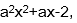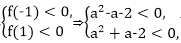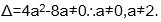- 一元二次不等式的解法
- 共209题
1
题型:
单选题
|
4.已知函数f(x)=
正确答案
C
解析
f(x)=
知识点
二次函数的图象和性质一元二次不等式的解法
1
题型:
单选题
|
5.已知命题p:方程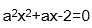
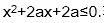
正确答案
B
解析
若命题“p∨q”为假命题,
则p假且q假.
当p假时,令f(x)=
则方程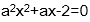
∴a=0或
故a∈(-1,1).
当q假时,
综上,a∈(-1,0)∪(0,1).
故选B.
知识点
命题的真假判断与应用一元二次不等式的解法
1
题型:
单选题
|
5.已知命题p:方程

正确答案
B
解析
若命题“p∨q”为假命题,
则p假且q假.
当p假时,令f(x)=
则方程
∴a=0或
故a∈(-1,1).
当q假时,
综上,a∈(-1,0)∪(0,1).
故选B.
知识点
命题的真假判断与应用一元二次不等式的解法
1
题型:
单选题
|
1.函数f(x)=
正确答案
A
解析
∵ 由1-x2≥0得-1≤x≤1,
又1-tan x>0,
∴ tan x<1,
∴ 
∴ 函数的定义域为
知识点
一元二次不等式的解法
1
题型:
单选题
|
10.不等式组
正确答案
A
解析
解析已在路上飞奔,马上就到!
知识点
一元二次不等式的解法
已完结
扫码查看完整答案与解析