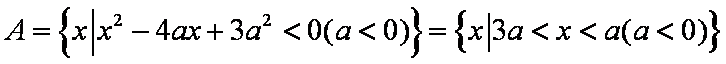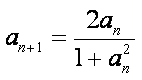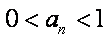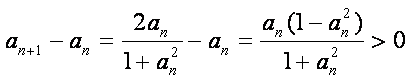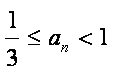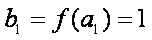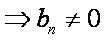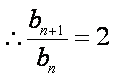- 一元二次不等式的解法
- 共209题
设命题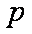
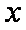
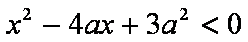
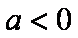
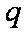
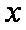
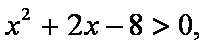

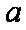
正确答案
见解析
解析
解析:设
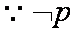
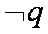

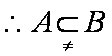
所以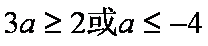
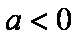
所以实数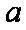
知识点
设集合A为函数y =ln(-x2-2x+8)的定义域,集合B为函数
y=x+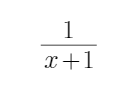
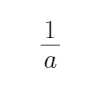
(1)求A∩B; (2)若
正确答案
见解析
解析
(1)由-x2-2x+8>0,解得A=(-4,2),又y=x+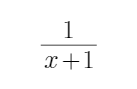
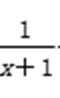
所以B=(-∞,-3]∪ [1,+∞),所以A∩B=(-4,-3]∪[1,2),
(2)因为∁RA=(-∞,-4]∪[2,+∞)。
由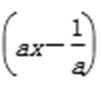
① 当a>0时,由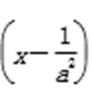

② 当a<0时,由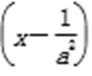
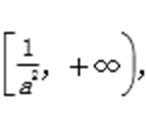
欲使C⊆∁RA,则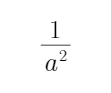
解得-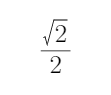
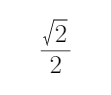
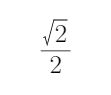
综上所述,所求a的取值范围是
知识点
函数




正确答案
解析
:结合三次函数的对称性,

知识点
在数列



(1)求证:数列
(2)设数列




正确答案
见解析
解析
证明:(1)∵

∴数列


(2)由(1)知

∴
∴
∴由②-①可得
∴
知识点
已知函数

(1)求不等式
(2)若不等式

正确答案
(1)
(2)
解析
(1)由题意得

∴ 
所以

(2) 因为
所以

∴
所以


知识点
已知函数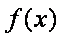
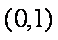
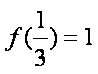
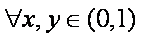
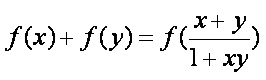
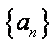
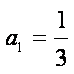
(1)证明: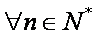
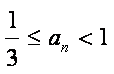
(2)若数列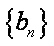
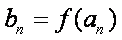
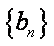
(3)设
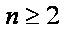
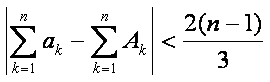
(其中符号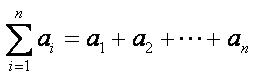
正确答案
见解析。
解析
(1)证明:依题意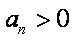
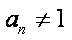
当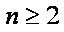
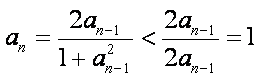
而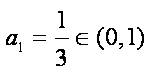
又
∴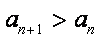
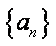
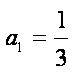
(2)由(1)有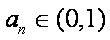
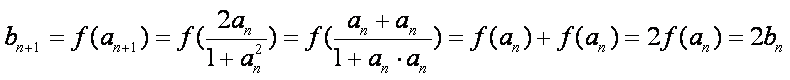
又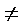
∴数列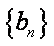
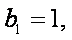
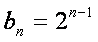
(3)由(1)知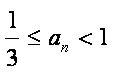
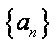
∴
当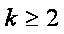
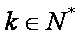
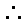
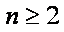
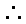
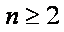
知识点
已知向量

(1)若


(2)在△ABC中,角A,B,C的对边分别是


正确答案
见解析
解析
解:
∵




∴

知识点
21.已知数列{






(1)证明:
(2)是否存在

正确答案
见解析。
解析
(1)由题设



(2)由题设


假设{



证明


数列奇数项构成的数列
令

数列偶数项构成的数列
令

∴

因此,存在存在

知识点
7. 不等式组









正确答案
解析
略
知识点
13.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析