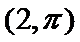- 平面直角坐标系与曲线方程
- 共4题
12.在直角坐标系


正确答案
解析
由极坐标方程得


考查方向
解题思路
先将极坐标方程两边同乘以
易错点
极坐标和直角坐标的互化公式记不住出错。
知识点
15.已知直线l的参数方程为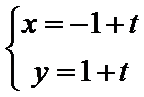
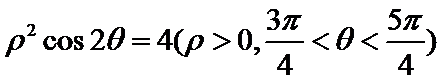
正确答案
解析
直线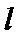
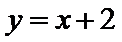
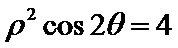
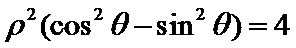
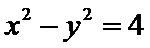
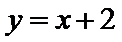
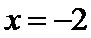
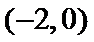
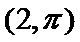
考查方向
解题思路
参数方程主要通过代入法或者已知恒等式(如
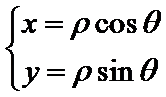
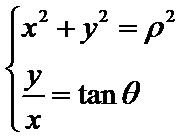
易错点
参数方程与普通方程的转化
知识点
选修4—4:坐标系与参数方程
在极坐标系中,曲线




(1)以极点为原点,极轴为x轴的正半轴,取与极坐标相同单位长度,建立平面直角坐标系,写出曲线L和直线
(2)求|BC|的长。
正确答案
见解析。
解析
解析:(1)由题意得,点

曲线L的普通方程为:
直线l的普通方程为:
(2)设B(


由韦达定理得

由弦长公式得
知识点
选修4-4:坐标系与参数方程(本小题满分10分)
选做题:
在直角坐标系







31.求曲线
32.若曲线




正确答案
对于曲线




正确答案
联立曲线






扫码查看完整答案与解析