- 等差数列的前n项和及其最值
- 共124题
1
题型:简答题
|
已知数列


21.求数列
22.设
第(1)小题正确答案及相关解析
正确答案
解析
(1)设数列






考查方向
考查等差数列的通项公式的求法
解题思路
运用从一般到特殊的处理方法,准确确定等差数列的通项公式。
第(2)小题正确答案及相关解析
正确答案
解析
(2)由(1)知,

得
考查方向
考查错位相减法求数列的前n项和,考查综合化简能力。
解题思路
对所得数学式子准确地变形,应用“错位相减法”求和。
易错点
错位相减后求和时,弄错数列的项数,或忘记从

1
题型:
单选题
|
9.已知等比数列



正确答案
C
解析
解:设等比数列{an}的公比是q,因为


考查方向
本题考查等比数列的通项公式,以及方程思想,属于基础题.
解题思路
设等比数列{an}的公比是q,根据题意和等比数列的通项公式列出方程,化简后求出q的值,即可求出a2
易错点
计算错误,主要是用换元法。
知识点
等差数列的前n项和及其最值
1
题型:
单选题
|
4.等差数列




正确答案
C
解析
因为





考查方向
本题主要考查了等差数列的通项公式及前n项和公式,为高考必考题,在近几年的各省高考题出现的频率较高,常与等差数列的定义、性质等知识点交汇命题。
解题思路
由已知
易错点
对等差数列的前n项和公式不熟悉导致出错。
知识点
等差数列的性质及应用等差数列的前n项和及其最值
1
题型:
单选题
|
3.已知等差数列
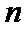
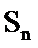
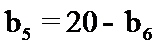
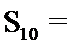
正确答案
C
解析
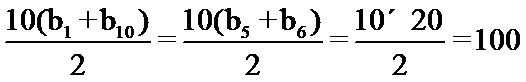
考查方向
本题主要考查了等差数列的性质及前n项和的应用
解题思路
利用等差数列的求和公式表示出前10项的和,再利用等差数列的性质即可解出。
易错点
不会利用等差数列的性质来求解。
知识点
等差数列的基本运算等差数列的前n项和及其最值
1
题型:
单选题
|
5. 设




正确答案
A
解析
由等差中项性质得:
考查方向
本题考察了数列的基本概念,等差数列的性质和前n项和。
解题思路
利用等差中项的概念,可以得到第三项,再利用前五项的和与第三项的关系可得。
易错点
利用前n项和公式,找不到前五项和和已知条件的关系。
知识点
等差数列的前n项和及其最值
已完结
扫码查看完整答案与解析