函数的最值
共119题

· 函数的最值

函数的最值
共119题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

已知函数f（x）＝｜lnx｝－1。

（1）当x＞0时，解不等式

（2）当，求函数的最大值；

（3）当x＞c时，有恒成立，求实数k的取值范围。

（注：e为自然对数的底数）。

正确答案

见解析。

解析

知识点

函数的最值

题型：简答题

简答题 · 16 分

已知为实数，函数.

（1）当时，求的最小值；

（2）当时，判断的单调性，并说明理由；

（3）是否存在小于的实数，使得对于区间上的任意三个实数、、，都存在以、、为边长的三角形，请说明理由.

正确答案

见解析

解析

易知的定义域为，且为偶函数.

（1）时,

时最小值为2.

（2）时,

时，递增；时，递减；

为偶函数.所以只对时，说明递增.

设，所以，得

所以时，递增；

（3），，

从而原问题等价于求实数的范围，使得在区间上，恒有

当时, ，为递增函数

由，得与矛盾.

所以不存在小于的实数，使得对于区间上的任意三个实数，都存在以为边长的三角形.

知识点

函数单调性的判断与证明函数的最值函数奇偶性的判断

题型：单选题

单选题 · 5 分

复数在复平面上所对应的点位于（）

A实轴上

B虚轴上

C第一象限

D第二象限

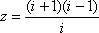
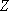
正确答案

解析

略

知识点

函数的最值

题型：单选题

单选题 · 5 分

若变量、满足约束条件则的最小值为

A17

B14

正确答案

解析

直线的交点分别为，代入目标函数得：，，，所以的最小值为

知识点

函数的最值

题型：简答题

简答题 · 12 分

图(5)是某市2月1日至14日的空气质量指数趋势图，空气质量指数(AQI)小于100表示空气质量优良，空气质量指数大于200表示空气重度污染，某人随机选择2月1日至2月12日中的某一天到达该市，并停留3天。

（1）求此人到达当日空气质量优良的概率;

（2）求此人停留期间至多有1天空气重度污染的概率。

正确答案

见解析。

解析

（1）在2月1日至2月12日这12天中，只有5日、8日共2天的空气质量优良，所以此人到达当日空气质量优良的概率.

（2）根据题意，事件“此人在该市停留期间至多有1天空气重度污染”，即“此人到达该市停留期间0天空气重度污染或仅有1天空气重度污染”.

“此人在该市停留期间0天空气重度污染”等价于“此人到达该市的日期是4日或8日或9日”.其概率为，

“此人在该市停留期间仅有1天空气重度污染”等价于“此人到达该市的日期是3日或5日或6日或7日或10日”.其概率为，

所以此人停留期间至多有1天空气重度污染的概率为.P=.-

知识点

函数的最值

题型：填空题

填空题 · 4 分

在△ABC中，角A,B,C所对的边分别为a，b，c，已知的面积为__________.

正确答案

解析

略

知识点

函数的最值

题型：单选题

单选题 · 5 分

设函数则f(f(3))＝(　　)

正确答案

解析

因为3＞1，所以.又因为，

所以.

于是，故选D项

知识点

函数的最值求函数的值

题型：填空题

填空题 · 5 分

已知函数若，则实数______；函数的最大值为_____。

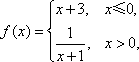
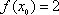
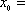
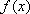
正确答案

-1;3

解析

略

知识点

函数的最值求函数的值

题型：简答题

简答题 · 14 分

已知向量，，其中.函数在区间上有最大值为4,设.

（1）求实数的值；

（2）若不等式在上恒成立，求实数的取值范围.

正确答案

（1）（2）

解析

（1）由题得

又开口向上，对称轴为，在区间单调递增，最大值为4,

所以，

（2）由（1）的他，

令,则以可化为,

即恒成立,

且,当,即时最小值为0,

知识点

函数的最值函数恒成立、存在、无解问题平面向量数量积的运算

题型：简答题

简答题 · 14 分

已知函数，，。

（1）若，试判断并用定义证明函数的单调性；

（2）当时，求函数的最大值的表达式。

正确答案

（1）在上是增函数（2）

解析

（1）判断：若，函数在上是增函数.

证明：当时，，

在上是增函数.

在区间上任取，设，

所以，即在上是增函数。

（2）因为，所以

当时，在上是增函数，

证明：当时，在上是增函数（过程略）

在在上也是增函数

当时，在上是增函数

证明：当时，在上是增函数（过程略）

所以当时，取得最大值为；

知识点

函数单调性的判断与证明函数的最值

继续学习学习下一知识点

下一知识点 : 奇函数

百度题库 > 高考 > 文科数学 > 函数的最值

扫码查看完整答案与解析