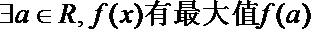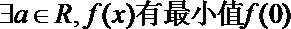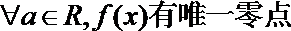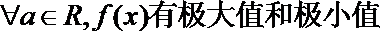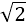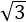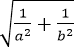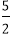- 函数的最值
- 共119题
1
题型:
单选题
|
9.已知函数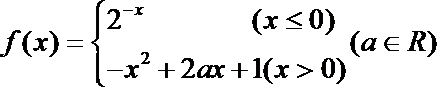
正确答案
C
解析
解析已在路上飞奔,马上就到!
知识点
命题的真假判断与应用分段函数的解析式求法及其图象的作法函数的最值
1
题型:填空题
|
10.若函数f(x)=x2-ax+2在区间[0,1]上至少有一个零点,则实数a的取值范围是___________.
正确答案
[3,+∞)
解析
由题意,知关于x的方程x2-ax+2=0在区间[0,1]上有实数解.
又x=0不是方程x2-ax+2=0的解,
所以根据0<x≤1可将方程x2-ax+2=0变形为a=

从而问题转化为求函数g(x)=x+
因为函数g(x)在(0,1]上单调递减,所以g(x)∈[3,+∞).
故所求实数a的取值范围是[3,+∞).
知识点
函数的最值
1
题型:
单选题
|
11.记min{a,b}为a、b两数的最小值,当正数x、y变化时,t=min{x,
正确答案
D
解析
(1)若x≤





(2)若






综上可知,当x=y=

知识点
函数的最值
1
题型:
单选题
|
4.若直线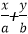
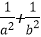
正确答案
B
解析
设向量m=(cosα,sinα),n=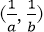
由题意知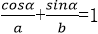
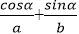
即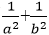
知识点
函数的最值利用基本不等式求最值
1
题型:
单选题
|
11.记min{a,b}为a、b两数的最小值,当正数x、y变化时,t=min{x,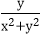
正确答案
D
解析
(1)若x≤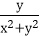
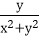
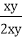
故t≤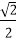
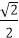
(2)若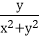
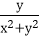
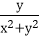
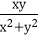

故t≤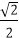
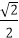
综上可知,当x=y=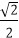
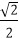
知识点
函数的最值
下一知识点 : 奇函数
扫码查看完整答案与解析