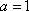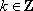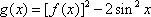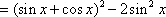- 函数的最值
- 共119题
已知函数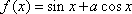
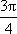
(1)求实数
(2)设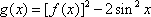
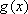
正确答案
(1)
(2)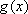
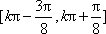
解析
(1)解:依题意,得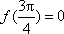
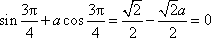
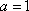
(2)解:由(1)得 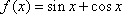
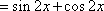
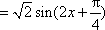
由 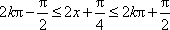
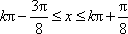
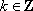
所以 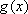
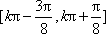
知识点
一同学为研究函数




正确答案
2
解析
略
知识点
已知定义在实数集







正确答案
解析
略
知识点
已知
(1)若


(2)若函数


(3)令





正确答案
见解析。
解析
(1)当






(2)函数



令



(3)假设存在实数



当




当








当










综上所述,存在实数


知识点
21。某旅游景点预计2013年1月份起前x个月的旅游人数的和p(x)(单位:万人)与x的关系近似地满足
(1)写出2013年第x月的旅游人数
(2)试问2013年第几月旅游消费总额最大,最大月旅游消费总额为多少元?
正确答案
见解析。
解析
(1)当

当


验证

(2)第
即
当



解得








当




综上,2013年第5月份的旅游消费总额最大,最大消费总额为3125万元. …12分
知识点
扫码查看完整答案与解析