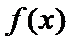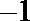- 函数的最值
- 共119题
10.下列函数中，其定义域和值域分别与函数y=10lgx的定义域和值域相同的是（ ）
Ay=x
By=lgx
Cy=2x
D
正确答案
解析
题目定义域与值域均为
考查方向
解题思路
基本初等函数的定义域、值域问题，应准确记忆图象，运用数形结合思想求解
易错点
题目
知识点
11.函数
正确答案
知识点
6．已知a函数f(x)=x3-12x的极小值点，则a=（ ）
正确答案
解析
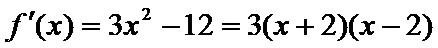
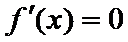
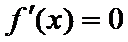
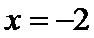
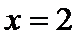
在（-2,2）上单调递减，在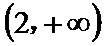
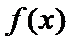
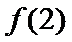
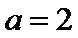
考查方向
解题思路
本题可以先求出函数的导数，然后解不等式得出函数的单调性，从而得出极值。
易错点
本题在求导判断极值点时易错。
知识点
6.已知
A
B
C
D
正确答案
解析
试题分析：由题意得
考查方向
解题思路
直接根据函数的性质进行判断.
易错点
对充分、必要条件的三种判断方法不清楚导致出错。
知识点
17.a为实数，函数
正确答案
解析
分类讨论得到
①
②：
③：
④：
综上，当
考查方向
解题思路
分类讨论来解答。
易错点
计算量大，讨论不清楚。
知识点
11．已知
A[-
B[-
C．[-
C[-
正确答案
解析
利用奇偶性作出函数的图像，观察得答案为A，
考查方向
解题思路
利用函数的图像观察出答案。
易错点
在解题时，主要出现了每一段的限制。
知识点
19.某公司计划购买1台机器，该种机器使用三年后即被淘汰. 机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元. 在机器使用期间，如果备件不足再购买，则每个500元.现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：
记x表示1台机器在三年使用期内需更换的易损零件数，y表示1台机器在购买易损零件上所需的费用（单位：元），n表示购机的同时购买的易损零件数.
(Ⅰ)若n=19，求y与x的函数解析式；
(Ⅱ)若要求“需更换的易损零件数不大于n”的频率不小于0.5，求n的最小值；
(Ⅲ)假设这100台机器在购机的同时每台都购买19个易损零件，或每台都购买20个易损零件，分别计算这100台机器在购买易损零件上所需费用的平均数，以此作为决策依据，购买1台机器的同时应购买19个还是20个易损零件？
正确答案
1
知识点
9.经市场调查，某超市的一种小商品在过去的近20天内的日销售量（件）与价格（元）均为时间t(天)的函数，且日销售量近似满足g(t)=80-2t（件），价格近似满足f(t)=20-
正确答案
1225
解析
因为y=g(t)·f(t)=(80-2t)(20-
所以当0≤t≤10时，y的取值范围是[1200，1225]
在t=5时，y取得最大值为1225；
当10≤t≤20时，y的取值范围是[600，1200]，
在t=10时，y取得最大值为1200.
知识点
13.已知
则
正确答案
0.8
解析
由于回归直线方程过样本中心点（x,y),根据表格数据，计算得到X=2,Y=2.6.代入回归直线方程，得到2.6=2k+1,k=0.8
考查方向
线性回归直线方程
解题思路
根据表格和直线回归方程求得
易错点
看不懂表格，对数据的提取有遗留
知识点
11．已知函数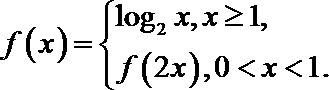
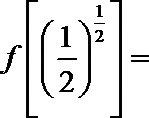
A
B
C1
D
正确答案
解析
因为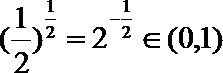
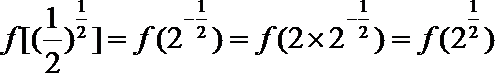
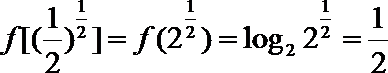
考查方向
本题主要考查了分段函数的求值、对数的运算。
易错点
本题易在判定
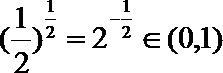
知识点
扫码查看完整答案与解析