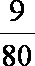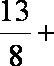- 函数的最值
- 共119题
若
(1)讨论
(2)当



正确答案
见解析。
解析
由
(1))令
则
①当


故
所以
所以

②当


故
所以
所以

③当

又因为

(i)当

当

所以

(ii) 当
令
令
故此时
减区间为
综上得:①当


②当

减区间为
③当


(2)因为在
所以
即
整理得
当
所以
知识点
已知函数
(1)求函数
(2)设











正确答案
(1)-2,
解析
解析:(1)
则

(2)








由余弦定理,得

由①②解得
知识点
如图,已知

(1)求异面直线

(2)求三棱锥

正确答案
(1)
解析


连接
则

由题意得


所以,异面直线

(2)由题意得,




三棱锥

知识点
数列



(1)当


(2)若数列

(3)当

正确答案
见解析
解析
(1)


(2)当

(3)





当

知识点
设函数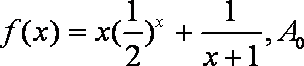
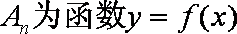
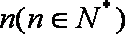
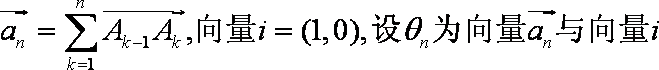

正确答案
3
解析
由题意知An=(n,f(n)),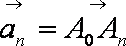
tanθn=
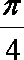
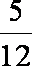
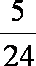
则有 1+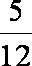
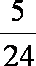
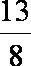

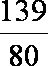
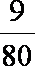
知识点
扫码查看完整答案与解析