- 函数的最值
- 共119题
已知函数
(1)求函数

(2)求
(3)设实数


正确答案
见解析。
解析
(1)



(2)令



当


(3)∵a>0,由(2)知:F(x)在(0,e)上单调递增,在(e,+∞)上单调递减,



当2<a时,
(3)另法:①2 a<e,即
②

1° 



③





知识点
设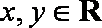
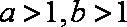
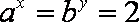
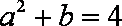
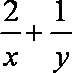
正确答案
解析
由题意得: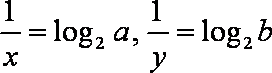
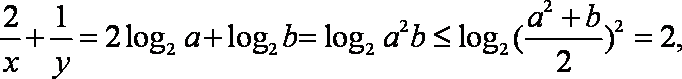
知识点
已知


(1) 求

(2)设函数




正确答案
(1)
解析
解析:(1)



∴



当

所以函数



(2)由(1)知:函数

∴ 
又 函数
① 当


②当





(3)当




∴

所以,

知识点
设递增等差数列






(1)求数列
(2)求数列


正确答案
见解析。
解析
在递增等差数列

解得 



知识点
已知函数
(1)若x<a时,f(x)<1恒成立,求实数a的取值范围;
(2)若a≥﹣4时,函数f(x)在实数集R上有最小值,求实数a的取值范围
正确答案
见解析。
解析
(1)因为x<a时,f(x)=4x﹣4×2x﹣a,所以令2x=t,则有0<t<2a,
所以f(x)<1当x<a时恒成立,可转化为
即
令

所以
所以

所以

所以
(2)当x≥a时,f(x)=x2﹣ax+1,即
①当
所以f(x)min=f(a)=1;
②当



所以由①②可得:当x≥a时有:
当x<a时,f(x)=4x﹣4×2x﹣a,令2x=t,t∈(0,2a),则
③当




④当

所以,此时,h(t)在(0,2a)上无最小值;
所以由③④可得当x<a时有:当

当
所以,由①②③④可得:
当


当
当﹣4≤a<0时,
综上所述,当


所以函数f(x)在实数集R上有最小值时,实数a的取值范围为
知识点
扫码查看完整答案与解析















