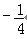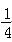- 函数的最值
- 共119题
1
题型：
单选题
|
若f（x）=asinx+b（a，b为常数）的最大值是3，最小值是﹣5，则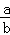
A﹣4
B4或﹣4
C
D
正确答案
B
解析
∵f（x）=asinx+b（a，b为常数）的最大值是3，最小值是﹣5，∴b+|a|=3，且 b﹣|a|=﹣5。
解得 b=﹣1，|a|=4，即 b=1，且a=±4，∴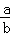
故选B。
知识点
函数的最值
1
题型：填空题
|
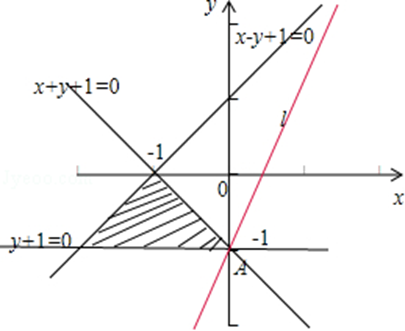
已知直线l分别过函数y=ax，（a＞0且a≠1）于函数y=logbx，（b＞0且b≠1）的定点，第一象限的点P（x，y）在直线l上，则﹣
正确答案
解析
由于函数y=ax，（a＞0且a≠1）与函数y=logbx，（b＞0且b≠1）的定点分别为（0，1），（1，0）
故由截距式得到直线l的方程为x+y=1，
又由第一象限的点P（x，y）在直线l上，则x+y=1，（x＞0，y＞0）
则
（当且仅当
故答案为
知识点
函数的最值
1
题型：
单选题
|
已知实数x，y满足条件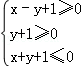
正确答案
C
解析
由约束条件作出图形：
易知可行域为一个三角形，验证当直线过点A（0，﹣1）时，
z取得最大值z=2×0﹣（﹣1）=1，
故选C
知识点
函数的最值
1
题型：
单选题
|
半径为4的球面上有A、B、C、D四点，AB，AC，AD两两互相垂直，则△ABC、△ACD、△ADB面积之和S△ABC+S△ACD+S△ADB的最大值为（ ）
正确答案
C
解析
根据题意可知，设AB=a，AC=b，AD=c，则可知AB，AC，AD为球的内接长方体的一个角，故a2+b2+c2=64，而
知识点
函数的最值
1
题型：
单选题
|
A2
B3
C3
D2
正确答案
D
解析
∵
则 m﹣（1﹣n）=0，即 m+n=1。
∴
当且仅当
故选D。
知识点
函数的最值
下一知识点 : 奇函数
扫码查看完整答案与解析