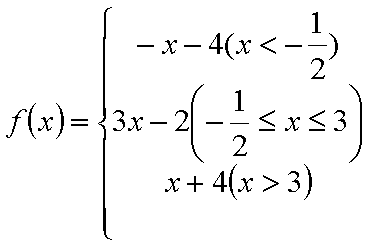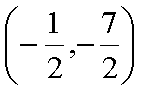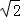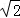- 函数的最值
- 共119题
设函数
(1)解不等式
(2)求函数
正确答案
见解析。
解析
(1)原不等式等价于不等式组


解得
(2)由(1)知
由函数
当

知识点
已知直线










(1)求椭圆
(2)若直线





(3)连接



正确答案
见解析
解析
(1)C:
(2)易知

由
又由

(3)m=0时,得N(

由(2)知A(x1,y1),B(x2,y2)于是 D(4,y1),E(4,y2),
先证直线AE过定点N:直线AE的方程为:
当x=
所以,点N在直线AE上,同理可得点N在直线BD上。即:m变化时, 直线AE与BD相交于定点N(
知识点
已知






正确答案
答案:12;-54
解析
略
知识点
设函数
(1) 求函数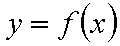
(2) 若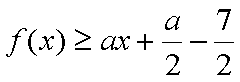
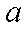
正确答案
见解析
解析
(1)由题意得
所以 f(x)在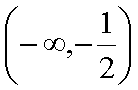
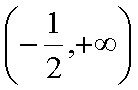
所以当
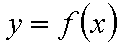
此时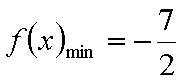
(2)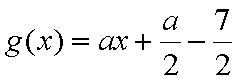
由图象可知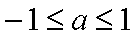
知识点
已知函数
(1)求
(2)求
正确答案
见解析。
解析
(1)

(2)
因为
当

当

知识点
我们把离心率之差的绝对值小于


正确答案
解析
双曲线




知识点
7.动圆C经过点F(1,0),并且与直线x=-1相切,若动圆C与直线y=x+2+1总有公共点,则圆C的面积( )
正确答案
解析
设圆心C(a,b),半径为r,r=|CF|=|a+1|,即(a-1)2+b2=(a+1)2,即







知识点
若实数x,y满足0<x≤2,0<y≤2,且使关于t的方程t2+2xt+y=0与t2+2yt+x=0均有实数根,则2x+y有( )
正确答案
解析
由于实数x,y满足0<x≤2,0<y≤2,且使关于t的方程t2+2xt+y=0与t2+2yt+x=0均有实数根,
则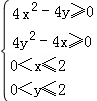
由z=2x+y得y=﹣2x+z,
平移直线y=﹣2x,由图象可知,
当直线y=﹣2x+z经过点A时,y=﹣2x+z的截距最小,此时z最小。
当直线y=﹣2x+z经过点B(2,2)时,y=﹣2x+z的截距最大,此时z最大。
由于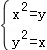
故z=2x+y有最小值3,最大值6。
知识点
已知向量


(1)求f (x)的最小正周期;
(2)求f(x)在
正确答案
(1)π
(2)最大值是1,最小值是
解析
f(x)=




(1)f(x)的最小正周期为
(2)∵0≤x≤
由正弦函数的性质,
当

当

当


∴f(x)的最小值为
因此,f(x)在
知识点
8.对向量a=(a1,a2),b=(b1,b2)定义一种运算“⊗”:a⊗b=(a1,a2)⊗(b1,b2)=(a1b1,a2b2).已知动点P,Q分别在曲线y=sin x和y=f(x)上运动,且



正确答案
解析
设P=(x1,y1),Q=(x,y),∵m=(
∴m⊗


∵


∴
∴

又y1=sin x1,∴

∴y=3sin(2x-

知识点
扫码查看完整答案与解析