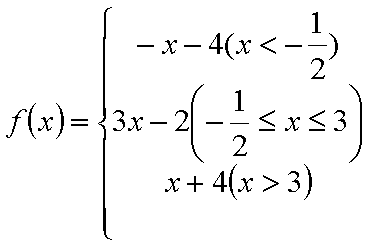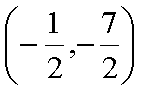- 函数的最值
- 共119题
设函数
(1)解不等式
(2)求函数
正确答案
见解析。
解析
(1)原不等式等价于不等式组


解得
(2)由(1)知
由函数
当

知识点
已知直线










(1)求椭圆
(2)若直线





(3)连接



正确答案
见解析
解析
(1)C:
(2)易知

由
又由

(3)m=0时,得N(

由(2)知A(x1,y1),B(x2,y2)于是 D(4,y1),E(4,y2),
先证直线AE过定点N:直线AE的方程为:
当x=
所以,点N在直线AE上,同理可得点N在直线BD上。即:m变化时, 直线AE与BD相交于定点N(
知识点
已知






正确答案
答案:12;-54
解析
略
知识点
设函数
(1) 求函数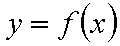
(2) 若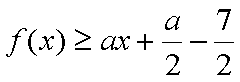
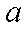
正确答案
见解析
解析
(1)由题意得
所以 f(x)在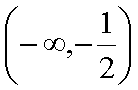
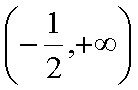
所以当
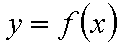
此时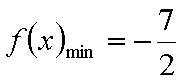
(2)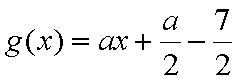
由图象可知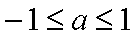
知识点
已知函数
(1)求
(2)求
正确答案
见解析。
解析
(1)

(2)
因为
当

当

知识点
扫码查看完整答案与解析