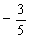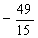- 同角三角函数基本关系的运用
- 共12题
在ABC中,角A、B、C的对边分别为a、b、c,已知
(1)求
(2)若

正确答案
见解析。
解析
(1)由a、b、c成等比数列,得
由正弦定理,得
所以
(2)由

又

所以
由余弦定理,得
代入数值,得

知识点
已知


正确答案
解析
略
知识点
已知函数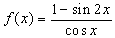
(1)求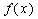
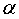
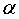

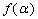
正确答案
见解析。
解析
解:(1)由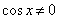
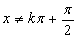
故
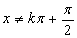
(2)由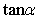
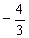
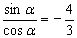
且α是第二象限的角, 解得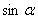
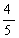
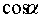
故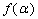
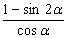
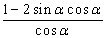
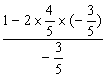
知识点
已知ΔABC的三个内角A、B,C满足


(1)求

(2)求函数

正确答案
见解析。
解析
(1)
∵
∴


又

又∵0°<A<180°, A=105°,B=60°,C=15°。……………………6分
(2)

可得
于是




知识点




(1)若

(2)若

正确答案
见解析。
解析
(1)

整理得:


∴
∴
(2)
整理得:
将上式平方得:
∴

整理得:
∴


知识点
扫码查看完整答案与解析