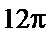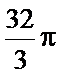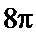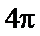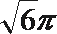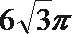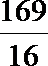- 立体几何与空间向量
- 共2637题
4. 体积为8的正方体的顶点都在同一球面上，则该球面的表面积为( )
A
B
C
D
正确答案
知识点
体积为8的正方体的顶点都在同一球面上，则该球面的表面积为( )
A
B
C
D
正确答案
知识点
16. 
正确答案
32
解析
如下图所示：
考查方向
解题思路
先求出球的半径再计算其表面积。
易错点
不会计算球的半径。
知识点
15．一个四面体的所有棱长都为
正确答案
解析
依题意，该四面体是棱长为
其外接球与正方体的外接球相同．易得正方体的棱长为1，其体对角线长即为外接球的直径，则
考查方向
解题思路
本题主要考查立体几何中组合体之间的关系，球的表面积公式等知识。
解题步骤如下：求出球的半径；利用公式求出球的表面积即可。
易错点
本题不易理解四面体的外接球与正方体的外接球相同这一事实，因而不能正确求出球的半径。
知识点
12. 四面体
A
B
C
D
正确答案
解析
如图，
考查方向
解题思路
因为AB
易错点
没有注意到垂直问题，以致于不能找出球的直径
知识点
10.已知A，B，C是球面上三点，且AB=6，BC=8，AC=10，球心O到平面ABC的距离等于该球半径的
A
B
C
D
正确答案
解析
△ABC的外接圆半径为5，且圆心在AC的中点处，又球心O到平面ABC的距离等于该球半径R的
考查方向
解题思路
先根据题目条件，画出图形，找到球心，再构造直角三角形，根据勾股定理计算出球的半径。
易错点
1、本题在确定球的球心时容易发生错误 。2、本题不容易找到球心的位置，导致题目无法进行。
知识点
10. 若一个球的体积是
正确答案
128
解析
由题可知，球的半径为4，则正方体的棱长为a,3a2=64,所以表面积为128.
考查方向
解题思路
表示球内接正方体的棱长，即可得到结果。
易错点
本题易在求棱长时发生错误。
知识点
8．平面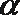
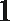
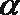
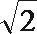
A
B
C
D
正确答案
解析
由题设截面圆圆心为H，则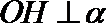
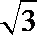
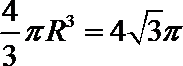
考查方向
本题主要考查球的相关知识。
解题思路
画出图形，归结到直角三角形中解决问题
易错点
不能画出正确图形，归结到直角三角形中解决问题。
知识点
10.点A，B，C，D在同一个球的球面上，AB = B
A
B8
C
D
正确答案
解析
AB=BC=AC=√3
∴四面体ABCD体积最大时,D在ABC的另一个半球内正△ABC面积=3√3/4
∴高=4
∴D到面ABC距离=4ABC所在面的圆心为O'球心为O
∴O'A=O'B=O'C=2√3×√3×sin60°=1设球的半径为R勾股定理得(4-R)²+1²=R²
解得R=17/8
∴表面积=4πR²=289/16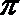
考查方向
本题主要与球体有关的计算、四面体体积最值问题。属于较难题
解题思路
先找到四面体体积最大时球的半径，然后再求表面积
易错点
找不到四面体体积最大时的情况，忘记球表面积计算公式
知识点
15. 
正确答案
解析
由题意画出几何体的图形如图，
把A、B、C、D扩展为三棱柱，上下底面中心连线的中点与A的距离为球的半径，
∴球半径AO=
考查方向
本题主要考查球的体积和表面积
解题思路
由题意把A、B、C、D扩展为三棱柱如图，求出上下底面中心连线的中点与A的距离为球的半径，然后求出球的表面积．
易错点
本题利用割补法结合球内接多面体的几何特征求出球的半径
知识点
11.已知球
A
B
C
D
正确答案
解析
设球O的半径为r，球心O在平面ABC上的射影为M，则M为三角形ABC的外心，由
考查方向
解题思路
先确定M为三角形ABC外接圆的圆心；利用平面几何的知识求出球O的半径，然后带入表面积公式即可。
易错点
不知道球心O在面ABC内的射影的位置；不会构建平面几何的知识求解半径。
知识点
14.已知球
正确答案
解析
求出球的半径为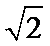
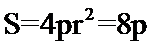
考查方向
解题思路
本题考查空间想象能力，解题步骤如下：先求球的半径再求出其表面积。
易错点
根据已知将球的半径求错。
知识点
11.已知四棱锥
A
B
C
D
正确答案
解析
由题意可得直观图如图所示，
因为
考查方向
解题思路
1)由已知条件画出草图；
2)找到球心的位置，以及构造直角三角形；
3)在直角三角形中计算球的半径，以及表面积.
易错点
本题由题意画出立体几何的图是一个难点，将立体的计算转化为平面也是难点。
知识点
7．如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是
正确答案
知识点
10. 球面上有三点A、B、C，任意两点之间的球面距离都等于球大圆周长的四分之一，且过这三点的截面圆的面积为
A
B
C
D
正确答案
解析
易得OA，OB，OC两两垂直且都为半径R，AB=AC=BC=
考查方向
解题思路
由已知条件先求出球的半径，在求求得体积。
易错点
熟悉等边三角形的性质，以及球面距离与大圆的关系。
知识点
扫码查看完整答案与解析