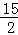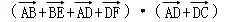立体几何与空间向量_章节学习

1

题型：填空题

|

填空题 · 4 分

16．四棱锥的底面是边长为的正方形，高为1，其外接球半径为，则正方形的中心与点之间的距离为．

正确答案

解析

可求得正方形的对角线长为4，设球心为，则到正方形的中心为，因为到正方形的距离为1，所以到正方形的中心距离与到球心的距离相等，则为.

考查方向

四棱锥的外接球问题，考察空间想象能力.

解题思路

求出球心到正方形的中心的距离，再结合图形判断位置关系求解.

易错点

球心位置的确定

知识点

棱柱、棱锥、棱台的体积与球体有关的内切、外接问题

1

题型：填空题

|

填空题 · 5 分

A，B两架直升机同时从机场出发，完成某项救灾物资空投任务.A机到达甲地完成任务后原路返回；B机路过甲地，前往乙地完成任务后原路返回.图中折线分别表示A，B两架直升机离甲地的距离s与时间t之间的函数关系. 假设执行任务过程中A,B均匀速直线飞行，则B机每小时比A机多飞行（）公里。

正确答案

20

解析

略

知识点

平面的基本性质及推论

1

题型：单选题

|

单选题 · 5 分

在空间，下列命题正确的是

A平行直线的平行投影重合

B平行于同一直线的两个平面平行

C垂直于同一平面的两个平面平行

D垂直于同一平面的两条直线平行

正确答案

D

解析

由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可以很容易得出答案。

知识点

平面的基本性质及推论平行公理空间中直线与直线之间的位置关系

1

题型：简答题

|

简答题 · 10 分

某地最近十年粮食需求量逐年上升，下表是部分统计数据：

（1）利用所给数据求年需求量与年份之间的回归直线方程;

（2）利用（1）中所求出的直线方程预测该地2012年的粮食需求量。

温馨提示：答题前请仔细阅读卷首所给的计算公式及说明.

正确答案

（1）（2）300（万吨）

解析

（1）由所给数据看出，年需求量与年份之间是近似直线上升，下面来配回归直线方程，为此对数据预处理如下：

对预处理后的数据，容易算得

由上述计算结果，知所求回归直线方程为

即 ①

（2）利用直线方程①，可预测2012年的粮食需求量为

（万吨）≈300（万吨）

知识点

平面的基本性质及推论

1

题型：单选题

|

单选题 · 5 分

三棱柱的侧棱与底面垂直，且底面是边长为2的等边三角形，其正视图（如图3所示）的面积为8，则该三棱柱外接球的表面积为

A

B

C

D

正确答案

C

解析

略

知识点

平面的基本性质及推论

1

题型：填空题

|

填空题 · 5 分

已知正方形的边长为，记以为起点，其余顶点为终点的向量分别为，，。若

且，则的所有可能取值为（）。

正确答案

-1，-2

解析

略

知识点

平面的基本性质及推论

1

题型：简答题

|

简答题 · 12 分

如图4，在直角坐标系xOy中，角α的顶点是原点，始边与x轴正半轴重合，终边交单位圆于点A，且.将角α的始边按逆时针方向旋转，交单位圆于点B，记.

（1）若；

（2）分别过A，B作x轴的垂线，垂足依次为C、D，记，求角的值.

正确答案

见解析。

解析

知识点

平面的基本性质及推论

1

题型：填空题

|

填空题 · 5 分

已知向量满足，则的夹角为_________.

正确答案

解析

略

知识点

平面的基本性质及推论

1

题型：填空题

|

填空题 · 5 分

一个四棱锥的三视图如图所示，其左视图是等边三角形，该四棱锥的体积= 。

正确答案

解析

略

知识点

平面的基本性质及推论

1

题型：填空题

|

填空题 · 5 分

已知菱形的边长为，，，则的值为。

正确答案

解析

略

知识点

平面的基本性质及推论

1

题型：填空题

|

填空题 · 5 分

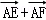
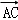
已知矩形ABCD中，AB=2，AD=1，E、F分别是BC、CD的中点，则（）•等于_________。

正确答案

解析

如图所示，

∵ 矩形ABCD中，E、F分别是BC、CD的中点，

∴ =，。

∴（）•=

====。

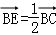
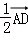
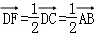
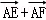
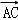
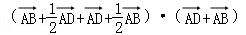
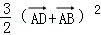
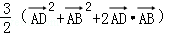
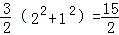
知识点

平面的基本性质及推论

1

题型：简答题

|

简答题 · 13 分

已知函数，，其中，为自然对数的底数。

（1）若在处的切线与直线垂直，求的值；

（2）求在上的最小值；

（3）试探究能否存在区间，使得和在区间上具有相同的单调性？若能存在，说明区间的特点，并指出和在区间上的单调性；若不能存在，请说明理由。

正确答案

见解析。

解析

（1），，

在处的切线与直线垂直，

………………………………………………………………3分

（2）的定义域为，且，

令，得， …………………………………………………………4分

若，即时，，在上为增函数，；………………………………………………………………………5分

若，即时，，在上为减函数，

； ……………………………………………………………6分

若，即时，

由于时，；时，，

所以

综上可知 ………………………………………8分

（3）的定义域为，且，

时，，在上单调递减，……………………………9分

令，得

①若时，，在上，单调递增，由于在上单调递减，所以不能存在区间，使得和在区间上具有相同的单调性；………………………………………………………………………………10分

②若时，，在上，单调递减；

在上，单调递增，由于在上单调递减，存在区间，使得和在区间上均为减函数，

综上，当时，不能存在区间，使得和在区间上具有相同的单调性；当时，存在区间，使得和在区间上均为减函数，…………………………………………………………………………………………13分

知识点

平面的基本性质及推论

1

题型：单选题

|

单选题 · 5 分

对于平面α和直线m、n，下列命题是真命题的是

A若m、n与α所成的角相等，则m//n

B若m//α，n//α，则m//n

C若m⊥α，m⊥n，则n//α

D若m⊥α，n⊥α，则m//n

正确答案

D

解析

略

知识点

平面的概念、画法及表示平面的基本性质及推论

1

题型：单选题

|

单选题 · 5 分

已知抛物线的准线与双曲线 (a>0，b>0)的两条渐近线分别交于A，B两点，O点坐标原点，若双曲线的离心率为2，则△AOB的面积S△AOB=

A

B

C

D4

正确答案

A

解析

略

知识点

平面的基本性质及推论

1

题型：单选题

|

单选题 · 5 分

已知、是不同的平面，、是不同的直线，则下列命题不正确的是

A若∥则.

B若∥则∥

C若∥，，则.

D若则∥.

正确答案

D

解析

略

知识点

平面的基本性质及推论

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点