- 立体几何与空间向量
- 共2637题
18.如图,在已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点E,连接PE并延长交AB于点G.
(I)证明G是AB的中点;
(II)在答题卡第(18)题图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
正确答案
(1)证明
∵ PD 

∵ DE

又∵ PD


∵ 正三棱锥P-ABC中PA=PB ∴ G为AB中点
(2)正三棱锥P-ABC中,PA=PB=PC ∵ 各侧面为直角三角形
∴PA



作EF//PB交PA于F 则EF
正三棱锥P-ABC中,D 为三角形ABC的重心,PA=6 ∴ AB=
∴DG=



∵ 


Rt

∴四面体PDEF体积
知识点
3.已知空间两条不同的直线


正确答案
解析
对于A:正确
对于B:正确应该是
对于C:
对于D:
考查方向
解题思路
本题属于常规题,可使用排除法解答,
易错点
该题易错于对判定定理不熟导致判断失误
知识点
19.如图,在三棱柱ABC-A1B1C1中,AB=AC,且侧面BB1C1C是菱形,∠B1BC=60°.
(Ⅰ)求证:AB1⊥BC;
(Ⅱ)若AB⊥AC,AB1=BB1,且该三棱柱的体积为2
正确答案
(Ⅰ)略(Ⅱ)AB=2
解析
(Ⅰ) 取BC的中点M,连接AM,B1M.
因为AB=AC, M是BC的中点,所以AM⊥BC
又因为侧面BB1C1C是菱形,且∠B1BC=60°
所以B1M⊥BC,
而AM∩B1M=M , AM, B1M
所以BC⊥平面AB1M,因为A B1
所以BC⊥AB1
(Ⅱ) 设AB=

因为 M是BC的中点,所以
又因为AB1=BB1, 所以
由(Ⅰ)知 B1M⊥BC,且AM∩BC=M,所以B1M⊥平面ABC,
即B1M为三棱柱ABC--A1B1C1的高,
所以三棱柱ABC--A1B1C1的体积V=Sh=
解得
考查方向
解题思路
解题步骤如下:在本题中,要证明两条异面直线垂直,需要证明一条直线垂直于另一条直线所在的平面,即需要线面垂直,即可得到线线垂直。根据题目给出的条件,知道体积,要求线段AB的长,联想到体积等于底面积乘以高,自然而然要去证明B1M为三棱柱ABC--A1B1C1的高,即可求出线段AB的长。
易错点
1、本题易在证明线面垂直时发生错误 。2、本题不容易得出B1M为三棱柱ABC--A1B1C1的高,导致题目无法进行。
知识点


正确答案
84
解析
∵


知识点
如图,在正方体ABCD﹣A1B1C1D1中,E、F、P、Q、M、N分别是棱AB、AD、DD1、BB1、A1B1、A1D1的中点,求证:
(1)直线BC1∥平面EFPQ;
(2)直线AC1⊥平面PQMN。
正确答案
略。
解析
(1)在正方体ABCD﹣A1B1C1D1中,连接AD1,
∵AD1∥BC1,且F、P分别是AD、DD1的中点,
∴FP∥AD1,∴BC1∥FP,
又FP⊂平面EFPQ,且BC1⊄平面EFPQ,
∴直线BC1∥平面EFPQ;
(2)如图,
连接AC、BD,则AC⊥BD,∵CC1⊥平面ABCD,BD⊂平面ABCD,
∴CC1⊥BD;
又AC∩CC1=C,∴BD⊥平面ACC1,
又AC1⊂平面ACC1,∴BD⊥AC1;
又∵M、N分别是A1B1、A1D1的中点,
∴MN∥BD,∴MN⊥AC1;
同理可证PN⊥AC1,
又PN∩MN=N,∴直线AC1⊥平面PQMN。
知识点
如图,四棱锥




(1)求证:
(2)求证:
正确答案
见解析。
解析
知识点
如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点。
(1)证明:PB∥平面AEC;
(2)设AP=1,AD=

正确答案
见解析。
解析
(1)证明:设BD与AC 的交点为O,连结EO,∵ABCD是矩形,∴O为BD的中点
∵E为PD的中点,∴EO∥PB,EO⊂平面AEC,PB⊄平面AEC∴PB∥平面AEC;
(2)∵AP=1,AD=



∴AB=
又
知识点
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1,连接AP交棱CC1于D。
(1)求证:PB1∥平面BDA1;
(2)求二面角A-A1D-B的平面角的余弦值;
正确答案
见解析
解析
解法一:
(1)连结AB1与BA1交于点O,连结OD,
∵C1D∥平面AA1,A1C1∥AP,∴AD=PD,又AO=B1O,
∴OD∥PB1,又OD面BDA1,PB1面BDA1,
∴PB1∥平面BDA1。
(2)过A作AE⊥DA1于点E,连结BE,∵BA⊥CA,BA⊥AA1,且AA1∩AC=A,
∴BA⊥平面AA1C1C,由三垂线定理可知BE⊥DA1。
∴∠BEA为二面角A-A1D-B的平面角。
在Rt△A1C1D中,
又

在Rt△BAE中,

故二面角A-A1D-B的平面角的余弦值为
解法二:
如图,以A1为原点,A1B1,A1C1,A1A所在直线分别为x轴,y轴,z轴建立空间直角坐标系A1-B1C1A,则




(1)在△PAA1中有

∴


设平面BA1D的一个法向量为
则


∵
∴PB1∥平面BA1D,
(2)由(1)知,平面BA1D的一个法向量
又

故二面角A-A1D-B的平面角的余弦值为
知识点
执行如图的程序框图,若输入n=3,则输出T= 。
正确答案
20
解析
由程序框图知:算法的功能是求T=1+(1+2)+(1+2+3)+…+(1+2+3+…+i)的值,
当输入n=3时,跳出循环的i值为4,
∴输出T=1+3+6++10=20。
知识点
5.设l是直线,α和β是平面,则下列说法正确的是( )
正确答案
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是简单。
考查方向
本题主要考查了线面位置关系,在近几年的各省高考题出现的频率较高。
解题思路
本题考查线面位置关系,解题步骤如下:
由题可知,A中可能l∥β;B中可能l在β内;C中可能α⊥β。
易错点
本题易在判断线是否在面上发生错误。
知识点
如图,四棱锥



(1)求证:
(2)求证:
正确答案
;见解析。
解析
(1)连接AC交BE于点O,连接OF,不妨设AB=BC=1,则AD=2

又
(2)


知识点
(如图,在四面体



(1) 求证:

(2) 求证:四边形
(3 是否存在点

正确答案
略
解析
(1)因为D,E分别为AP,AC的中点,
所以DE//PC。
又因为DE
所以DE//平面BCP。
(2)
因为D,E,F,G分别为AP,AC,BC,PB的中点,
所以DE//PC//FG,DG//AB//EF。
所以四边形DEFG为平行四边形,
又因为PC⊥AB,所以DE⊥DG,
所以四边形DEFG为矩形。
(3)存在点Q满足条件,理由如下:连接DF,EG,设Q为EG的中点,
由(2)知,DF∩EG=Q,且QD=QE=QF=QG=
分别取PC,AB的中点M,N,连接ME,EN,NG,MG,MN。
与(2)同理,可证四边形MENG为矩形,其对角线点为EG的中点Q,
且QM=QN=
知识点
设集合A={


正确答案
解析

知识点
如图,在四棱台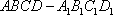
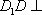
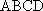
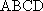
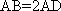
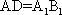
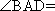
(1)证明: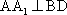
(2)证明: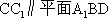
正确答案
见解析。
解析
(1)证明:因为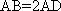
AD=a,则AB=2a,又因为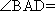
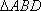
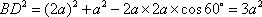
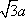

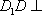
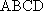


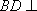
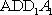
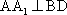
(2)连结AC,设AC
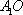
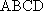
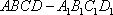
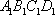
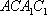
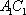
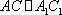
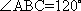
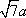
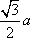
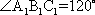
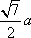
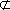


知识点
设





正确答案
解析
知识点
扫码查看完整答案与解析