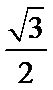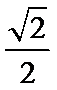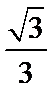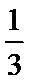- 立体几何与空间向量
- 共2637题
如图所示的几何体是由以正







20.求证:直线

21.求直线

正确答案
见解析
解析
(1)证:取DE的中点G,连结GF.由三棱柱得,AF//BD//CE,
∵OG为梯
而CE//AF,且AF=2 ∴OG
∴四边形OAFG为平行四边形 ∴GF//OA
又OA

考查方向
解题思路
该题解题关键在于找到所求内容的突破点
取DE的中点G,连结GF.由三棱柱得,AF//BD//CE,得到OG为梯
易错点
本题容易在辅助线建立过程出错,空间直角坐标系建立及其坐标表示出错
正确答案
见解析
解析
(2)∵

又
在面BCED中,过C作
∴
在ΔCFH中,


∴直线FC和面DEF所成角的正弦值为
注:解法2可用等积法;解法3可用空间直角坐标系
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
通过在面BCED中,过C作


易错点
本题容易在辅助线建立过程出错,空间直角坐标系建立及其坐标表示出错
19. 如图,在三棱锥P-AMC中,AC=AM=PM=2,PM⊥面AMC,AM⊥AC,B,D分别为CM,AC的中点.
(Ⅰ)在PC上确定一点E,使得直线PM∥平面ABE,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,连接AE,与PD相交于点N,求三棱锥B-ADN的体积.
正确答案
(1)E为PC的中点;(2)
解析
试题分析:本题属于立体几何证明与求体积的问题,(1)利用线面垂直的判定定理来证明;(2)将体积最终转化为
(Ⅰ)E为PC的中点.理由如下:
连接BE,由于B,E分别为CM,PC的中点,
所以BE∥PM,
又BE

所以PM∥面ABE.
(Ⅱ)由于AE,PD分别是△PAC的边PC,AC上的中线,所以AE和PD的交点N为△PAC的重心,故N为PD靠近D的三等分点,
则
而因为D为AC的中点,所以
又由于E为PC的中点,
所以
所以三棱锥B-AND的体积为
考查方向
解题思路
本题考查立体几何证明与求体积的问题,解题步骤如下:
(1)利用线面垂直的判定定理来证明;
(2)将体积最终转化为
易错点
求体积的时候不会转化。
知识点
19. 如图,空间几何体








(1)试确定点


(2)在(1)的条件下,平面



正确答案
(1)M是线段AE的中点,证明见解析;(2)
解析
试题分析:本题属立体几何中的有关证明和体积有关的计算问题,题目的难度是逐渐由易到难,(1)根据线面平行的判定定理来证明;(2)将2个几何体的体积计算出来再计算出比值。
试题解析:(Ⅰ)当M是线段AE的中点时,AC//平面MDF,证明如下: 1
连结CE交DF于N,连结MN,由于M、N分别是AE、CE的中点,
所以MN//AC,又MN在平面MDF内, 所以AC//平面MDF (

三棱柱ADE-



又 三棱锥F-DEM的体积


考查方向
解题思路
本题考查了立体几何中的有关证明和体积有关的计算问题,解题步骤如下:(1)根据线面平行的判定定理来证明;(2)将2个几何体的体积计算出来再计算出比值。
易错点
不会求体积。
知识点
如图,在三棱柱





20.求证:

21.求证:平面

正确答案
(Ⅰ)略.
解析
(Ⅰ)连接



在三棱柱
四边形


又∵


又∵



∴

考查方向
解题思路
先根据题中给出的条件证明
易错点
不会从图中找与直线
正确答案
(Ⅱ)略.
解析
(Ⅱ)∵



∵


∵



∵





∵

∵




∴

∵

∴平面

考查方向
解题思路
先证明

易错点
找不到哪条线垂直于那个平面导致根本没有思路。
22.已知









(Ⅰ)求证:
(Ⅱ)若




正确答案
见解析
知识点
如图,在四棱锥









21.求证:

22.求三棱锥
正确答案
详见解析
解析
考查方向
线面平行的证明
解题思路
由线线平行、面面平行证明线面平行
易错点
立体感不强,逻辑关系混乱
正确答案
详见解析
解析
考查方向
求立体几何体的体积
解题思路
先求出E到平面DFC的距离,然后计算几何体的体积
易错点
找不到点到平面的距离,计算能力弱
8. 在平行四边形








正确答案
解析
根据题意,

考查方向
平面向量的基本定理及性质
解题思路
由基本不等式即可得出2λ+μ的范围,从而便可得出2λ+μ的最大值.
易错点
对平面向量的性质掌握不好,计算能力弱
知识点
甲和乙系夫妻,乙已经怀孕,一日甲和乙二人去郊外春游时发生车祸,甲当场死亡,乙被送往医院,早产婴儿丙,丙生存数小时就因缺氧导致死亡,后乙昏迷数日也死亡。甲生前拥有大笔财产,其弟丁,其兄戊健在,乙只有一个其父母收养的妹妹己,则对甲的财产分配正确的是( )。
A.丁1/4、戊1/4、己1/2
B.全部由戊继承
C.己1/2和戊1/2
D.全部由己继承
正确答案
D
解析
[考点] 继承应注意的相关问题 [解析] 《继承法》第10条规定了法定继承的顺序:第一顺序:配偶、子女、父母。第二顺序:兄弟姐妹、祖父母、外祖父母。继承开始后,由第一顺序继承人继承,第二顺序继承人不继承。没有第一顺序继承人继承的,由第二顺序继承人继承。 另外,虽然我国法律规定自然人的权利能力始于出生,终于死亡,但《继承法》第28条规定了胎儿的继承份额:遗产分割时,应当保留胎儿的继承份额。胎儿出生时是死体的,保留的份额按照法定继承办理。《最高人民法院关于贯彻执行(中华人民共和国继承法>若干问题的意见》第45条进一步规定:应当为胎儿保留的遗产份额没有保留的,应从继承人所继承的遗产中扣回。为胎儿保留的遗产份额,如胎儿出生后死亡的,由其继承人继承;如胎儿出生时就是死体的,由被继承人的继承人继承。 在本题中,“甲和乙二人去郊外春游时发生车祸,甲当场死亡”,而题目中的甲并没有留有遗嘱,因此,甲的财产按照法定继承由其第一顺序继承人继承,甲的第一顺序继承人为乙,同时依照胎儿继承的相关规定,为胎儿丙保留遗产份额。因此,甲留有的财产先分割夫妻共同财产,则乙可以拥有财产的1/2,另外1/2由甲的第一顺序继承人乙继承(1/2)/2,另外的(1/2)/2属于为胎儿丙保留的份额,胎儿的份额是与乙平分的。这是第一层法律关系。 之后,早产婴儿生存数小时就因缺氧导致死亡,依照上文提到的相关法律的规定,应由丙的继承人继承其份额,按照法定继承的继承J顷序,丙的继承人为其母乙。因此,乙继承了丙的财产后,其继承财产总额为 (1/2)/2+(1/2)/2,再加上乙的个人财产,则乙现在拥有甲死亡时的全部财产。这是第二层法律关系。 “乙昏迷数日也死亡”,从题中得知,乙只有一个其父母收养的妹妹己,而《继承法》第10条第5款规定:本法所说的兄弟姐妹,包括同父母的兄弟姐妹、同父异母或者同母异父的兄弟姐妹、养兄弟姐妹、有抚养关系的继兄弟姐妹。因此,己具有继承权,可以继承乙的所有财产。则甲的全部财产至此全部由己继承,选项D“全部由己继承”是正确答案。
依据《安全生产法》规定,危险物品的生产、经营、储存单位以及矿山、建筑施工单位的主要负责人和安全生产管理人员,应当由有关主管部门对其( )考核合格后方可任职。考核不得收费。
A.安全生产知识
B.安全评价常识
C.管理能力
D.操作能力
E.作业资格
正确答案
A,C
解析
暂无解析
18.如图





(1)证明:

(2)证明:
(3)求点

正确答案
(1)由四边形



(2)先证



(3)取












试题解析:
(1)因为四边形






(2)因为四边形











(3)取































解析
解析已在路上飞奔,马上就到!
知识点
11.平面α过正方体ABCD-A1B1C1D1的顶点A,α//平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为( )
正确答案
知识点
函数f(x)=
正确答案
解析
由y=f(x)=


∵x>0,∴y>0.
∴f-1(x)=
知识点
若x,y满足约束条件
正确答案
0
解析
z=-x+y⇒y=x+z,z表示直线y=x+z在y轴上的截距,截距越小,z就越小,画出题中约束条件表示的可行域(如图中阴影部分所示),当直线过点A(1,1)时,zmin=0.
知识点
16. 设x,y,z是空间中不同的直线或不同的平面,且直线不在平面内,则下列结论中能保证“x⊥z,且y⊥z ,则 x//y ”为真命题的是______________________(请把你认为所有正确的结论的代号都填上).
①x为直线,y, z为平面; ②x , y , z为平面; ③x , y为直线,z为平面;
④x , y , z为直线; ⑤x , y为平面,z为直线.
正确答案
①③⑤
解析
易知①正确;由垂直于同一平面的两条直线平行,可得③由垂直于同一条直线的两个平面平行,可得⑤正确,当x , y , z为平面时,存在两两垂直的三个平面,如正方体从一定点出发的三个平面。因而②是错误的;当x , y , z为直线时,存在两两垂直的三条直线,如正方体从一定点出发的三条棱。因而④是错误的。
考查方向
解题思路
利用线面垂直的判定定理与性质定理,逐一判断各个命题是否正确。
易错点
不熟悉常用结论,推理失误出错。
知识点
如图,正三棱柱ABC—A1B1C1中,D是BC的中点,AA1=AB=1.
21.求证:A1C//平面AB1D;
22.求二面角B—AB1—D的大小;
正确答案
解法一:证明:连接A1B,设A1B∩AB1 = E,连接DE.
∵ABC—A1B1C1是正三棱柱,且AA1 = AB,
∴四边形A1ABB1是正方形,
∴E是A1B的中点,又D是BC的中点, ∴DE∥A1C. ……………… 4分
∵DE

解法二:
如图,
证明:
连接A1B,设A1B∩AB1 = E,连接DE.
设A1A = AB = 1,
则



考查方向
解题思路
利用三角形中位线定理证明DE//A1C,再利用线面平行的判定定理证明
易错点
熟悉线面平行的判定定理
正确答案
解析
解法一:在面ABC内作DF⊥AB于点F,在面A1ABB1内作FG⊥AB1于点G,连接DG.
∵平面A1ABB1⊥平面ABC, ∴DF⊥平面A1ABB1,
∴FG是DG在平面A1ABB1上的射影, ∵FG⊥AB1, ∴DG⊥AB1
∴∠FGD是二面角B—AB1—D的平面角 …………………………8分
设A1A = AB = 1,在正△ABC中,DF=
在△ABE中,

所以,二面角B—AB1—D的大小为
解法二:


设

故
同理,可求得平面AB1B的法向量是
设二面角B—AB1—D的大小为θ,
∴二面角B—AB1—D的大小为
考查方向
解题思路
先作出二面角的平面角,再证明,最后计算。(一作、二证、三计算)
易错点
熟悉二面角的计算
扫码查看完整答案与解析