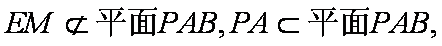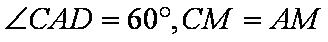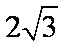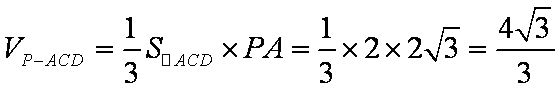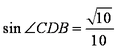- 立体几何与空间向量
- 共2637题
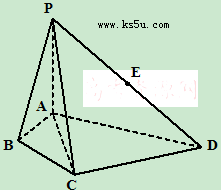
如图,在四棱锥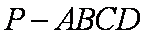
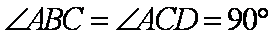
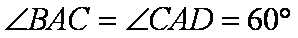
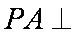
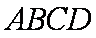
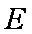
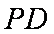
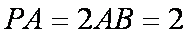
(1)求证: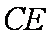
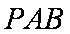
(2)求四面体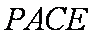
正确答案
见解析
解析
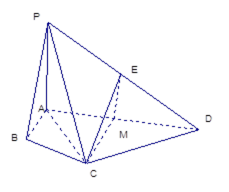
证明:(1)取AD得中点M,连接EM,CM.则EM//
因为
所以,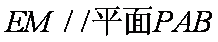
在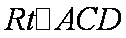
所以,
而
因为
所以,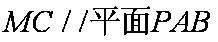
又因为
所以,
因为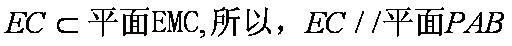
(2)由已知条件有;AC=2A
因为,
因为E是PD的中点,所以,四面体PACE的体积
知识点
已知




正确答案
解析
略
知识点
如图,


所在的平面垂直于该半圆所在平面,且
(1)求证:
(2)设平面
①求证:

②若

正确答案
见解析
解析
(1)∵E是半圆上异
又∵矩形平面ABCD⊥平面ABE,且CB⊥AB,
由面面垂直性质定理得:CB⊥平面ABE,∴平面CBE⊥平面ABE,
且二面交线为EB,由面面垂直性质定理得:
AE⊥平面ABE,又EC在平面ABE内,故得:EA⊥EC
(2) ①由CD//AB,得CD//平面ABE,又∵平面CDE∩平面ABE于直线EF,∴根据线面平行的性质定理得:
CD//EF,CD//AB,故EF//AB
②分别取AB、EF的中点为O、M,连接OM,则在直角三角形OME中,







则
知识点
在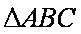
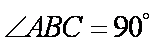
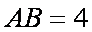
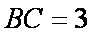
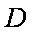
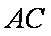
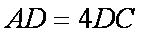
(1)求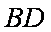
(2)求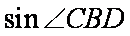
正确答案
(1)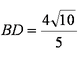
解析
解析:
(1)解:因为 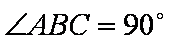
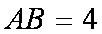
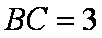
所以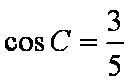
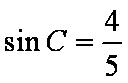
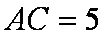
又因为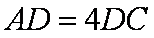
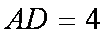
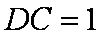
在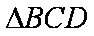
得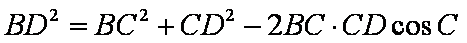
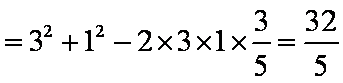
所以 
(2)在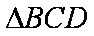
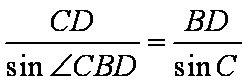
所以 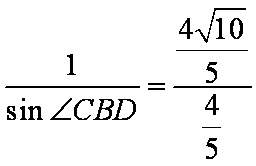
所以 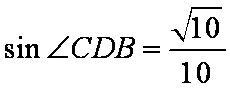
知识点
在

(1)若

(2)若

正确答案
(1)
解析
(1)方法一:因为 

所以 


又因为 

所以 
所以 
所以 
因为 
所以 
所以 
方法二: 因为 
所以 
因为 

所以 
所以 
所以 
所以 
所以 
因为 
所以 
所以 

(2)因为 

所以 
所以 


因为 
所以 
所以 
所以 
所以 当

………………13分
知识点
在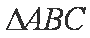
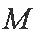
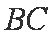
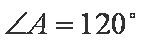
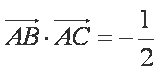
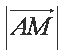
正确答案
解析
略
知识点
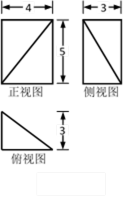
若某几何体的三视图(单位: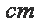
正确答案
解析
略
知识点
如图,在三棱柱







(1)求证:

(2)求证:

(3)在棱




正确答案
见解析
解析
(1)连结



在




所以

又因为



所以

(2)因为侧棱



所以
又因为



因为


所以
因为



又因为



所以

所以
因为
所以

(3)当点




设



因为



所以


又因为

所以


所以

因为

所以

又因为



知识点
如图1,在梯形











(1)求证:
(2)求证:

(3)判断直线

正确答案
见解析
解析
解析
(1)因为 四边形
所以
因为 平面





所以 

因为 

所以 
(2)证明:因为 四边形
所以 
因为 


所以 平面


因为 

所以 

(3)直线

取






所以 

在矩形


所以 

所以 

所以 四边形
所以 

因为 四边形



所以 

所以 四边形
所以 

所以

所以 
所以 

因为 
所以 四边形


所以 直线

知识点
某几何体的三视图如图1所示,且该几何体的体积是

正确答案
解析
略
知识点
已知复数z满足
正确答案
解析
略
知识点
如图, 已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且
求证:(1)EC⊥CD ;
(2)求证:AG∥平面BDE;
(3)求:几何体EG-ABCD的体积。
正确答案
见解析
解析
(1)证明:由平面ABCD⊥平面BCEG,
平面ABCD∩平面BCEG=BC, 

又CD
(2)证明:在平面BCDG中,过G作GN⊥CE交BE于M,连
DM,则由已知知;MG=MN,MN∥BC∥DA,且



∵DM


(3)解:

知识点
下列四个图中,函数
正确答案
解析
略
知识点
某圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为
正确答案
2π
解析
略
知识点
设

正确答案
1+
解析
略
知识点
扫码查看完整答案与解析