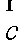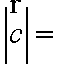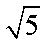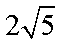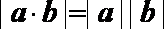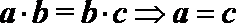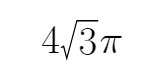- 立体几何与空间向量
- 共2637题
如图,













(1) 求证:



(2) 求证:
正确答案
见解析。
解析
(1)连结


则

则



(2)由直角三角形的射影原理可知
由




则

知识点
一个体积为
正确答案
解析
略
知识点
已知向量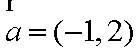
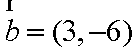
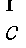

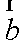
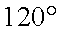
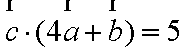
正确答案
解析
略
知识点
一个三条侧棱两两互相垂直并且侧棱长都为a的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为
正确答案
解析
由题可知该三棱锥为一个棱长



知识点
如图,










(1) 求证:平面

(2) 求四棱锥
正确答案
见解析。
解析
(1) 证明:由题可知,

(2)
则
知识点
不等式x-2y+6>0表示的区域在直线x-2y+6=0的
正确答案
解析
右下方为不等式所表示区域,故选B.
知识点
已知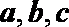
① 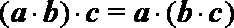
③ 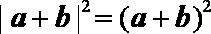
正确答案
解析
由平面向量的基础知识可知①②④均不正确,只有③正确,故选A.
知识点
如图所示是一个几何体的三视图,则该几何体的体积为
正确答案
解析
由图可知该几何体是由两个相同的半圆柱与一个长方体拼接而成,因此
知识点
A、B、C三点在同一球面上,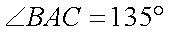
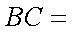
正确答案
解析
略
知识点
如图,已知AB为圆O的一条直径,以端点B为圆心的圆交直线AB于C、D两点,交圆O
于E、F两点,过点D作垂直于AD的直线,交直线AF于点H。
(1)求证:B、D、H、F四点共圆;
(2)若
正确答案
见解析
解析
(1)因为

又

(2)因为AH与圆B相切于点F,
由切割线定理得
所以
又△AFB∽△ADH,所以
由此得
连接BH,由(1)知,BH为△BDF外接圆的直径,
故△BDF的外接圆半径为
知识点
已知i为虚数单位,复数

正确答案
解析
略
知识点
如图,四棱锥






(1) 求证:
(2) 在棱



(3) 求点

正确答案
见解析
解析
解:
(1)方法一:取


△

所以

又




所以



所以
方法二:连结




又



又




所以

又


(2)当点


证明如下:
取棱





所以



所以
(3)点



由(1)可知








即

在


在


边

所以

设点





所以
解得



知识点
如图所示,矩形长为3,宽为2,在矩形内随机撒200颗黄豆,数得落在椭圆内的黄豆数为160颗,依据此实验数据可以估计出椭圆的面积约为
正确答案
4.8
解析
略
知识点
某几何体的三视图如图所示,则该几何体的体积是
正确答案
解析
略
知识点
某空间几何体的三视图如图所示,则该几何体的表面积为( )
正确答案
解析
由三视图知:几何体是直三棱柱,且三棱柱的高为4,
底面是直角边长为2的等腰直角三角形,斜边长为

∴几何体的表面积S=2×



知识点
扫码查看完整答案与解析