- 立体几何与空间向量
- 共2637题
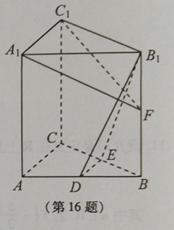
16.(本小题满分14分)
如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且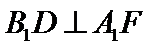
求证:
(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
正确答案
知识点
9.某几何体的三视图如图所示(单位:cm),则该几何体的表面积是______cm2,体积是______cm3.
正确答案
80 ;40.
知识点
如图,在四棱锥P-ABCD中,PA⊥CD,AD∥BC,∠ADC=∠PAB=90°,BC=CD=½AD。
(I) 在平面PAD内找一点M,使得直线CM∥平面PAB,并说明理由;
(II)证明:平面PAB⊥平面PBD。
正确答案
(I)取棱AD的中点M(M∈平面PAD),点M即为所求的一个点.理由如下:
因为AD‖BC,BC=
所以四边形AMCB是平行四边形,从而CM‖AB.
又AB

所以CM∥平面PAB.
(说明:取棱PD的中点N,则所找的点可以是直线MN上任意一点)
(II)由已知,PA⊥AB, PA ⊥ CD,
因为AD∥BC,BC=
所以PA ⊥平面ABCD.
从而PA ⊥ BD.
因为AD∥BC,BC=
所以BC∥MD,且BC=MD.
所以四边形BCDM是平行四边形.
所以BM=CD=
又AB∩AP=A,所以BD⊥平面PAB.
又BD
所以平面PAB⊥平面PBD.
知识点
19.
如图,四棱锥P-ABCD中,PA⊥地面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(I)证明MN∥平面PAB;
(II)求四面体N-BCM的体积.
正确答案
(Ⅰ)由已知得







又




因为





(Ⅱ)因为



所以


取





由




所以四面体

知识点
18.如图,在四棱锥


(I)求证:平面
(II)求三棱锥
正确答案
(1)见解析;
(2)
解析
本题属于立体几何应用中的基本问题,题目的难度不大,用到一些平面几何的知识。
(1)化为求线面垂直
(2)转变思想,换个角度看问题。
(I)连接BQ,因为ABCD是直角梯形,AD∥BC,AD=2BC,Q为AD的中点,
所以BCDQ为平行四边形,又因为CD=

因为ΔPAD是边长为2的正三角形,Q是AD的中点,
所以PQ⊥AD,PQ=
在ΔPQB中,QB=


因为AD∩BQ=Q,AD、BQ
所以PQ⊥平面ABCD.
因为PQ
(II)由(I)知:PQ⊥平面ABCD,PQ=
因为底面ABCD为直角梯形,AD∥BC,∠ADC=
所以ΔBCD是直角三角形,其中∠BCD=
因为BC=1,CD=

考查方向
本题考查了空间面面垂直、求椎体体积等知识,全面考查了学生阅读能力、空间想象能力与分析问题解决问题的能力,属于中档题,立体几何也是高考的必考内容,常与平几知识相结合,也有的会需要建立空间坐标系,结合空间向量的知识解决。
易错点
第二问求三棱锥的体积,如果不知道转化,则无法求出.
知识点
18. 如图所示,该几何体是由一个直三棱柱



(Ⅰ)证明:平面

(Ⅱ)求正四棱锥


正确答案
略
解析
(Ⅰ)证明:直三棱柱









(Ⅱ)




考查方向
本题考查了立体几何中的面面垂直的证明和正四棱锥的体积问题,
解题思路
本题第一问证明面面垂直,只要证明线面垂直即可;第二问把两个几何体的体积求出来,由两个几何体的体积关系直接求出高就行了。
易错点
1、解题 的规范化问题,2、第二问中不能正确的求出所需几何体的体积。
知识点
19.已知在四棱锥S—ABCD中,底面ABCD是平行四边形,若SB丄AC,SA = SC.
(1)求证:平面SBD丄平面
(2)若 AB = 2,SB = 3,cos∠SCB=
正确答案
如图所示
(1)设AC∩BD=O,
连接SO
因为SA=SC,
所以SO∩SB=S,所以AC⊥平面SBD,
因为AC在平面ABCD内,
所以平面SBD⊥平面ABCD
(2)作SH⊥平面ABCD,即
由(1)知,AC⊥BD,
所以底面ABCD是菱形,
所以BC=AB=2
因为SB=3,cos∠SCB=1/8
所以由余弦定理可得,
SC=2,所以∠SAC=60°,
所以SAC是等边三角形
所以在Rt△SOH中,SH=SO*sin60°=3/2
所以
解析
证AC垂直于面ABCD,
设AC交BD于0,
因为SA=SC,
SO交SB于S,
所以AC垂直于平面SBD,
因为AC在平面ABCD内,
所以面SBD垂直于面ABCD.求底面面积时,
先用余弦定理求出角SOB=120度,角SOH=60度,
所以四棱锥的体积为
考查方向
立体几何中的相关计算和证明
解题思路
通过线线垂直得到线面垂直,进而得到面面垂直,找清四棱锥的底面和高,利用公式求解。
易错点
面面垂直概念混淆,立体感不强
知识点
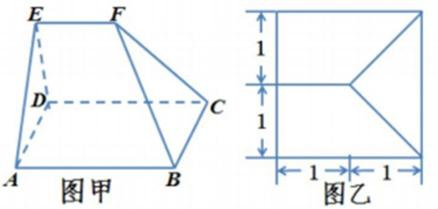
16. 多面体ABCDEF(如图甲)的俯视图如图乙,己知面ADE为正三角形.
(1)求多面体ABCDEF的体积;
(2)求证:平面ACF⊥平面BDF.
正确答案
(1)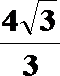
(2)略.
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难.
(1)分别取AB、CD的中点M、N,连接EM、EN、MN,多面体体积转化为棱柱AED-MFN的体积V1与四棱锥F-MBCN的体积V2之和。
由三视图可知,AD=2,AM=DN=1,面ADE为正三角形且垂直于底面ABCD,知F点到底面的距离为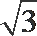
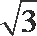
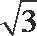
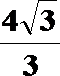
考查方向
本题考查了立体几何中的体积和面面垂直的问题.属于高考中的高频考点。
解题思路
本题考查立体几何中的体积和面面垂直的问题,解题步骤如下:
(1)做辅助线,拆分多面体。
(2)转化为证明线面垂直。
易错点
(1)第一问中的多面体的拆分。
(2)第二问中的面面垂直的转化。。
知识点
19.如图,四棱柱








(Ⅰ)证明:平面

(Ⅱ)若


正确答案
见解析
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难.
试题解析:(Ⅰ)依题意


∵








(Ⅱ)取






∴四边形
可得



即异面直线


考查方向
本题考查了立体几何中的面面垂直和异面直线所成的角的问题.属于高考中的高频考点。
解题思路
本题考查立体几何,解题步骤如下:
(1)转化为证明线面垂直。
(2)找到三角形,利用余弦定理求解。
易错点
(1)第一问中的面面垂直的转化。(2)第二问中异面直线所成的角求解时要找到适当的三角形。
知识点
正确答案
知识点
7.若




正确答案
解析
若










考查方向
解题思路
利用直线与平面平行于垂直的关系,结合充分条件和必要条件性质,判断关系。
易错点
逻辑混乱,直线与平面的位置关系掌握不牢
知识点
如图,在直三棱柱




且

17.直线

18.平面

正确答案



又





解析



又





考查方向
解题思路
易错点
判定定理的选用,线面关系的转化
正确答案



且



又

又

又







解析



且



又

又

又







考查方向
解题思路
易错点
判定定理的选用,线面关系的转化
7.如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )
正确答案
解析
由题意可知是上面是圆锥下面是圆柱的组合体,圆柱的侧面积为



考查方向
解题思路
以三视图为载体考查几何体的还原及表面积,解题的关键是根据三视图想象原几何体的形状构成,并从三视图中发现几何体中各元素间的位置关系及数量关系,然后分步对各部分表面积求解.
易错点
圆锥的侧面积公式,底面积的个数易错。
知识点
16.如图,已知直三棱柱






(1)求证:

(2)求证:平面

正确答案
详见解析
解析
试题分析:本题是空间中平行与垂直的基本问题,题目的难度是逐渐由易到难,证明的关键是按照线面平行、面面垂直的判定,找到使定理成立的条件,所以空间中的读图能力,熟练把握空间中垂直关系的判定与性质是解题的突破口。
证明:(1)在




所以
又





(2)因为



又




所以

而


又




所以

又



考查方向
解题思路
本题考查空间中平行与垂直的证明
1、证明线面平行时,关键是设法在平面内找到一条直线与已知直线平行。
2、证明面面垂直本质是转化为证线面垂直,关键是在证线面垂直时,找到两条线是相交直线与已知直线垂直,同时熟练把握空间中垂直关系的判定与性质。
易错点
1、第一问中的易忽视线面平行中线在面外。
2、第二问中证明面面垂直本质是转化为证线面垂直,不要忽视证线面垂直时,两条线是相交直线,同时熟练把握空间中垂直关系的判定与性质。
知识点
6.某四面体的三视图均为直角三角形,如图所示,则该四面体的表面积为( )
正确答案
解析
将三视图还原为直方图如图所示,
这时底面积为


考查方向
解题思路
将三视图还原为直方图如图所示,利用已知条件可求得。
易错点
还原直观图出现问题。
知识点
扫码查看完整答案与解析