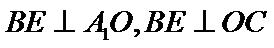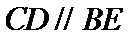- 立体几何与空间向量
- 共2637题
19.
如图,四棱锥P-ABCD中,PA⊥地面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(I)证明MN∥平面PAB;
(II)求四面体N-BCM的体积.
正确答案
知识点
如图,已知





19.求证:EF∥平面
20.求证:平面

21.求直线

正确答案
要证明EF∥平面

证明:如图,连接





解析
见答案.
考查方向
易错点
线面关系与面面关系的转化
正确答案
要证明平面



因为AB=AC,E为BC中点,所以










解析
见答案.
考查方向
易错点
线面垂直于面面垂直的转化.
正确答案

解析
取









取

























考查方向
易错点
线面角定义的灵活运用
13.如图,在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,



正确答案
知识点
13.如图,在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,



正确答案
知识点
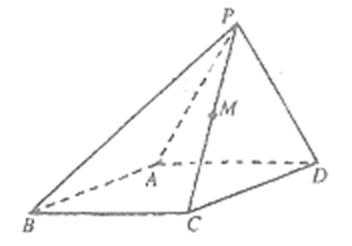
如图,在四棱锥P-ABCD中,PA⊥CD,AD∥BC,∠ADC=∠PAB=90°,BC=CD=½AD。
(I) 在平面PAD内找一点M,使得直线CM∥平面PAB,并说明理由;
(II)证明:平面PAB⊥平面PBD。
正确答案
(I)取棱AD的中点M(M∈平面PAD),点M即为所求的一个点.理由如下:
因为AD‖BC,BC=
所以四边形AMCB是平行四边形,从而CM‖AB.
又AB

所以CM∥平面PAB.
(说明:取棱PD的中点N,则所找的点可以是直线MN上任意一点)
(II)由已知,PA⊥AB, PA ⊥ CD,
因为AD∥BC,BC=
所以PA ⊥平面ABCD.
从而PA ⊥ BD.
因为AD∥BC,BC=
所以BC∥MD,且BC=MD.
所以四边形BCDM是平行四边形.
所以BM=CD=
又AB∩AP=A,所以BD⊥平面PAB.
又BD
所以平面PAB⊥平面PBD.
知识点
11.平面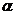
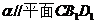
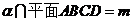
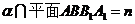
正确答案
知识点
16.如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且

求证:(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
正确答案
(1)


又





⑵ 


且



又

又

又







知识点
6.已知函数F(x)=ex满足F(x)=g(x)+h(x),且g(x)和h(x)分别是R上的偶函数和奇函数,若∀x∈[1,2]使得不等式g(2x)-ah(x)≥0恒成立,则实数a的取值范围是( )
正确答案
解析
由F(x)=g(x)+h(x)=ex,得F(-x)=g(-x)+h(-x)=e-x
即F(-x)=g(x)-h(x)=e-x
解得g(x)= 

∀x∈[1,2],g(2x)-ah(x)≥0恒成立,即得

分离参数得a≤


因为ex-e-x+


即ex-e-x=

知识点
18.在直三棱柱ABC﹣A1B1C1中,AB=AC=AA1=3,BC=2,D是BC的中点,F是C1C上一点.
(1)当CF=2,求证:B1F⊥平面ADF;
(2)若FD⊥B1D,求三棱锥B1﹣ADF体积.
正确答案
(1)见证明;(2)
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:
(1)证明:∵AB=AC,D是BC的中点,
∴AD⊥BC.在直三棱柱ABC﹣A1B1C1中,
∵B1B⊥底面ABC,AD⊂底面ABC,∴AD⊥B1B.
∵BC∩B1B=B,∴AD⊥平面B1BCC1.
∵B1F⊂平面B1BCC1,∴AD⊥B1F.
在矩形B1BCC1中,∵C1F=CD=1,B1C1=CF=2,
∴Rt△DCF≌Rt△FC1B1.
∴∠CFD=∠C1B1F.∴∠B1FD=90°,∴B1F⊥FD.
∵AD∩FD=D,∴B1F⊥平面ADF.
(2)解:∵AD⊥面B1DF,
又
∵FD⊥B1D,∴Rt△CDF∽Rt△BB1D,∴
∴
∴
考查方向
解题思路
(1)利用相关定理进行证明;
(2)利用等体积法即可求解.
易错点
相关定理不熟容易处错。
知识点
18.如图,在三棱柱




(Ⅰ)求证:
(Ⅱ)求点

正确答案
(1)略;
(2)
【发呢之】12
解析
试题分析:本题第(1)问属于空间线面垂直关系的判定,是基础知识,难度中等;第(2)问是空间距离的问题,可以用等体积法进行解答。解答过程如下:
(Ⅰ)因为



在
由余弦定理得:







(Ⅱ)

考查方向
解题思路
1、第(1)问根据线面垂直的性质定理可证,在平面ABC中寻找两条与C1B垂直的直线即可;
2、第(2)问可以通过把求距离的问题转化为求高的问题,用等体积法进行解答。
易错点
在解决第二问时不能很好地对图形进行转化而导致失误。
知识点
如图1,在直角梯形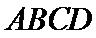


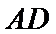



19.证明: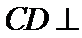
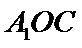
20.当平面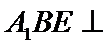
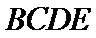
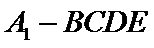

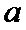
正确答案
(Ⅰ) 略.
解析
试题分析: (Ⅰ) 在图1中,因为

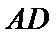
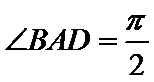
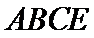
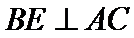
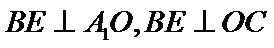
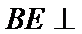
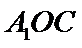
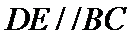

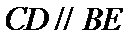
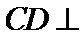
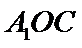
(Ⅰ)在图1中,因为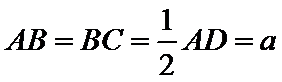
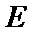
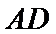

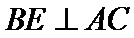
即在图2中,
从而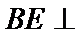
又
所以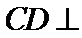
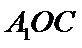
考查方向
解题思路
在处理有关空间中的线面平行.线面垂直等问题时,常常借助于相关的判定定理来解题,同时注意恰当的将问题进行转化
易错点
线线关系与线面关系的转换
正确答案
(Ⅱ) 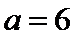
解析
试题分析:(Ⅱ)由已知,平面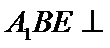
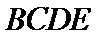

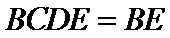
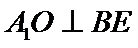
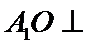
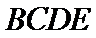
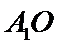
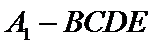
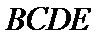
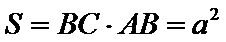
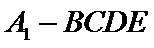
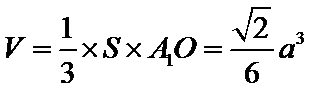
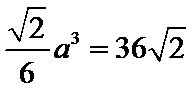
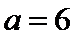
(Ⅱ)由已知,平面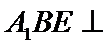
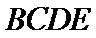
且平面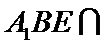
又由(Ⅰ)知,
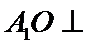
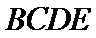
即
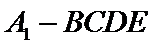
由图1可知,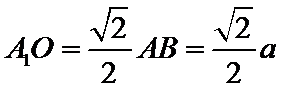
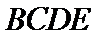
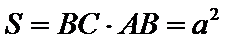
从而四棱锥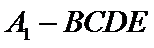
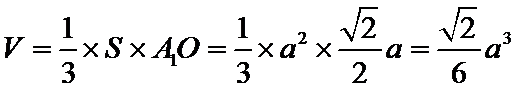
由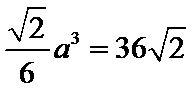
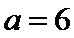
考查方向
解题思路
2.求几何体的体积的方法主要有公式法.割补法.等价转化法等,本题是求四棱锥的体积,可以接使用公式法.
易错点
体积的计算
如图





21.证明:

22.证明:
23.求点

正确答案
(1)证明见解析;
解析
(1)因为四边形






考查方向
解题思路
(1)由四边形




















易错点
定理的条件不完整,书写格式不规范。
正确答案
(2)证明见解析;
解析
(2)因为四边形











考查方向
解题思路
(1)由四边形




















易错点
定理的条件不完整,书写格式不规范。
正确答案
(3)
解析
(3)取































考查方向
解题思路
(1)由四边形




















易错点
定理的条件不完整,书写格式不规范。
如图,四棱锥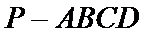
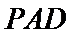
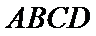
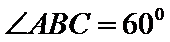
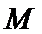
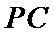
22.求证: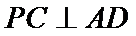
23.求点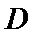
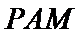
正确答案
(1)略;
解析
(1):取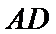
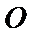
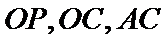
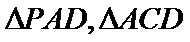
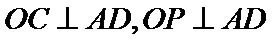
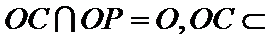
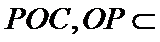
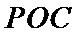
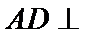
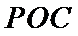
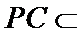
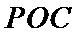
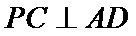
考查方向
解题思路
先证明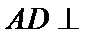
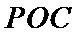
易错点
不会做辅助线导致没有思路;
正确答案
(2)
解析
(2)点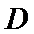
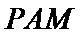
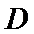
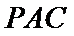
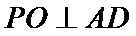
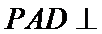
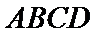
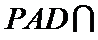

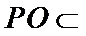
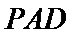
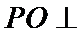
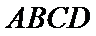
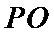
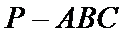
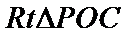
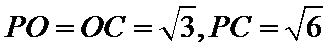
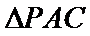
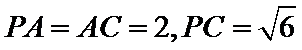
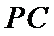
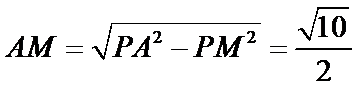
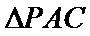
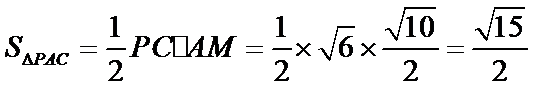
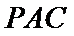
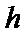
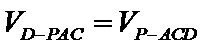
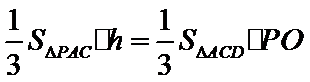
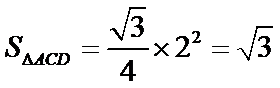
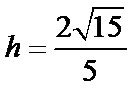
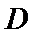
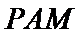
考查方向
解题思路
先发现点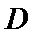
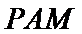
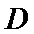
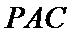
易错点
看不出点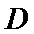
19. 如图,在矩形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
(Ⅰ)若E为BD的中点,求证:
正确答案
(1)见解析;(2)
解析
试题分析:本题属于立体几何的证明与体积的计算问题,
(1)由已知条件然后结合线面平行的判定定理来证明;
(2)将底面换了之后再来计算其体积。
(1)证明:取



又






(2)在平面图形




考查方向
解题思路
本题考查立体几何的证明与体积的计算问题,解题步骤如下:
(1)由已知条件然后结合线面平行的判定定理来证明;
(2)将底面换了之后再来计算其体积。
易错点
不会换底去计算体积。
知识点
4.设



正确答案
解析
试题分析:根据线面垂直,线面平行,面面平行的关系逐个进行判断。
对于A,∵l⊥



对于B,当



对于C,当l∥



对于D,当



考查方向
解题思路
A根据线面垂直的判定定理得出A正确;B根据面面垂直的性
质判断B错误C根据面面平行的判断定理得出C错误;D根据面面平行的性质判断D错误.
易错点
要考虑到空间直线,平面可能出现的各种关系.
知识点
扫码查看完整答案与解析