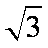- 立体几何与空间向量
- 共2637题
如图,在四棱锥





(1)求证:平面

(2)若平面





正确答案
见解析
解析
(1)证明:由条件

又
所以平面
(2)VM-BCDQ=

知识点
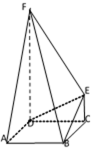
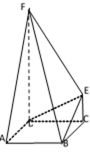
如图,FD垂直于矩形ABCD所在平面,CE//DF,
(1)求证:BE//平面ADF;
(2)若矩形ABCD的一个边AB =



正确答案
见解析
解析
解(1)过点E作CD的平行线交DF于点M,连接AM。
因为CE//DF,所以四边形CEMD是平行四边形,可得EM = CD且EM //CD,于是四边形BEMA也是平行四边形,所以有BE//AM,而直线BE在平面ADF外,所以BE//平面ADF,
(2)由EF =
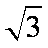

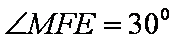
由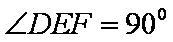
因为


所以,
因为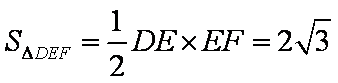


综上,当
知识点
已知椭圆









(1)求直线
(2)是否存在这样的椭圆,使得以

正确答案
见解析
解析
解:(1)离心率

设


整理得 





直线
(2)∵




代入椭圆方程,整理得
又设
假设存在这样的椭圆,使得以

得

知识点
已知
(1)若


(2)若



正确答案
(1)
(2)
解析
(1)由

所以 向量

(2)
知识点
如图所示的多面体中,正方形





(1)求证:

(2)求直线

正确答案
见解析。
解析
解法1:(1)取
















又

(2)作



由(1)知平面

从而




易知

于是




解法2:易知

故以


则
所以


(1)

又

(2)设面

由

又



对于任意

知识点
如图,P为△AOB所在平面上一点,向量



正确答案
解析
知识点
如图,几何体ABC一EFD是由直三棱柱截得的,EF //AB,
∠ABC=90°,AC=2AB = 2,,CD=2AE=
(1)求三棱锥D-BES的体积;
(2)求证:CE⊥DB
正确答案
见解析。
解析
(1)

可证EF⊥平面BCD,

(2)证明:连接
依题意:

又在

①②

知识点
如图,在四棱锥




(1)求证:
(2)若点

正确答案
见解析。
解析
(1)由
又


(2)取

则


从而四边形
故
知识点
如图,






(1)求证:

(2)求证:平面

正确答案
见解析。
解析
(1)取












∴ 




故
(2)



又




由(1)知



故
知识点
如图,在四棱锥S-ABCD中,底面ABCD是矩形,SA

(1)求证:SB∥平面ACM;
(2)求证:平面SAC
正确答案
见解析
解析
解:(1)连接BD,交AC于点O,连接MO,


MO


(2) 




























知识点
已知圆C过点(1,0),且圆心在x轴的正半轴上,直线l:y=x-1被该圆所截得的弦长为
正确答案
(x-3)2+y2=4
解析
待定系数法求圆的方程。
知识点
若某几何体的三视图(单位:cm)如图所示,则该几何体的体积为_________cm3。
正确答案
解析
由三视图知, 该几何体为圆柱上面加上一个圆锥,所以体积为
知识点
向量

正确答案
解析
设向量

则向量

知识点
已知
(1)求函数

(2)对一切

正确答案
见解析
解析
(1)
当

① 


② 




所以
(2)

设
① 
② 
所以

所以
知识点
已知直线
(1)



正确答案
解析
对于(1),由


知识点
扫码查看完整答案与解析