立体几何与空间向量_章节学习

1

题型：单选题

|

单选题 · 5 分

5．空间四边形ABCD的两条对角线AC和BD的长分别为6和4，它们所成的角为900，则四边形两组对边中点的距离等于（）

A

B

C5

D以上都不对

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

棱锥的结构特征异面直线及其所成的角

1

题型：单选题

|

单选题 · 5 分

已知>0，，直线=和=是函数图像的两条相邻的对称轴，则=

A

B

C

D

正确答案

A

解析

由题设知，=，∴=1，∴=（），

∴=（），∵，∴=，故选A.

知识点

棱锥的结构特征

1

题型：单选题

|

单选题 · 5 分

已知实数满足则的最大值是。

A

B

C

D

正确答案

C

解析

画图可知，四个角点分别是，可知

知识点

棱锥的结构特征

1

题型：单选题

|

单选题 · 5 分

若一个三棱锥的三视图如图所示，其中三个视图都是直角三角形，则在该三棱锥的四个面中，直角三角形的个数为

A

B

C

D

正确答案

D

解析

略

知识点

棱锥的结构特征简单空间图形的三视图

1

题型：填空题

|

填空题 · 5 分

在平面直角坐标系中，过坐标原点的一条直线与函数的图象交于P、Q两点，则线段PQ长的最小值是________

正确答案

4

解析

略

知识点

棱锥的结构特征

1

题型：填空题

|

填空题 · 5 分

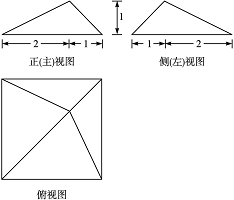
某四棱锥的三视图如图所示，该四棱锥的体积为__________。

正确答案

3

解析

由三视图知该四棱锥底面为正方形，其边长为3，四棱锥的高为1，根据体积公式V＝×3×3×1＝3，故该棱锥的体积为3.

知识点

棱锥的结构特征简单空间图形的三视图棱柱、棱锥、棱台的体积

1

题型：单选题

|

单选题 · 5 分

已知三棱锥中，底面为边长等于2的等边三角形，垂直于底面，=3，那么直线与平面所成角的正弦值为

A

B

C

D

正确答案

D

解析

过A作AE垂直于BC交BC于E，连结SE，过A作AF垂直于SE交SE于F，连BF，∵正三角形ABC，∴ E为BC中点，∵ BC⊥AE，SA⊥BC，∴ BC⊥面SAE，∴ BC⊥AF，AF⊥SE，∴ AF⊥面SBC，∵∠ABF为直线AB与面SBC所成角，由正三角形边长3，∴ ，AS=3，∴ SE=，AF=，∴

知识点

棱锥的结构特征

1

题型：简答题

|

简答题 · 12 分

在如图所示的几何体中，平面平面，四边形为平行四边形，，，，.

（1）求证：平面；

（2）求三棱锥的体积。

正确答案

见解析。

解析

（1）∵平面平面,且平面平面

平面平面 …………2分

, …………3分

又, …………4分

且,∴平面. …………………6分

（2）设AC的中点为G，连接EG，

由（1）可知平面，即 ,

又平面 ………8分

平面，

所以点F到平面的距离就等于点E到平面的距离

即点F到平面的距离为EG的长 …………………10分

即三棱锥的体积为 …………12分

知识点

棱锥的结构特征

1

题型：单选题

|

单选题 · 5 分

设是定义在上的增函数，且对于任意的都有恒成立。如果实数满足不等式,xxk那么的取值范围是

A(9, 49)

B(13, 49)

C(9, 25)

D(3, 7)

正确答案

A

解析

由得，又，

∴，

∵是上的增函数，∴＜，

∴. 结合图象知为圆内的点到原点距离，故.

∴.

知识点

棱锥的结构特征

1

题型：填空题

|

填空题 · 5 分

已知一个圆锥的母线长为2，侧面展开是半圆，则该圆锥的体积为

正确答案

解析

略

知识点

棱锥的结构特征

1

题型：简答题

|

简答题 · 14 分

16.如图，在直三棱柱ABC-A1B1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且，.

求证：（1）直线DE∥平面A1C1F；

（2）平面B1DE⊥平面A1C1F.

正确答案

(1)为中点，为的中位线

又为棱柱，

，又平面，且

平面；

⑵ 为直棱柱，平面

，又

且，平面

平面，

又，平面

又平面，

又，，且平面

平面，又

平面平面．

知识点

棱锥的结构特征

1

题型：填空题

|

填空题 · 5 分

16．关于正四棱锥,给出下列命题:

①异面直线所成的角为直角；

②侧面为锐角三角形；

③侧面与底面所成的二面角大于侧棱与底面所成的角；

④相邻两侧面所成的二面角为钝角；

其中正确的命题序号是___________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用棱锥的结构特征异面直线及其所成的角线面角和二面角的求法

1

题型：填空题

|

填空题 · 5 分

15.已知三棱锥内接于球，，当三棱锥的三个侧面的面积之和最大时，球的表面积为______.

正确答案

解析

试题分析：根据题意可知当三条侧棱互相垂直时三个侧面积之和最大，此时球的直径为以为边的正方体的体对角线长，所以球的半径，所以，故此题答案为。

考查方向

本题主要考椎体的外接球问题及球的表面积公式．

解题思路

根据题意可知当三条侧棱互相垂直时侧面积之和最大，进而求出球的表面积。

易错点

不知何时三个侧面积之和最大导致出错。

知识点

棱锥的结构特征

1

题型：简答题

|

简答题 · 12 分

18. 如图，在四棱锥中，是边长为的正三角形，，为棱的中点.

（1）求证:;

（2）若平面平面，，求点到平面的距离.

正确答案

（1）见证明；（2）

解析

试题分析：本题属于立体几何的综合应用问题，属于中档题，只要掌握相关立体几何的知识，即可解决本题，解析如下：

证明：取中点，连接、

∴,

∵

∴

∵、平面，、平面

∴平面平面

∵平面

∴平面

（Ⅱ）∵平面平面，

∴平面

∵平面

∴平面平面

∴在中，过作交延长线于点，则的长为点到平面的距离，

设点到的距离为，

则有,即

∴，即点到平面的距离为

考查方向

本题考查了线面平行、面面垂直、点到面的距离等知识点。

解题思路

（1）直接利用线面平行的判定定理进行证明；

（2）利用作出高，再利用体积公式即可求解．

易错点

知识点

棱锥的结构特征

1

题型：填空题

|

填空题 · 5 分

16.已知四棱锥的顶点都在球上，底面是矩形，平面平面，为正三角形，，则球的表面为______．

正确答案

解析

令三角形PAD所在圆的圆心为P，则圆P的半径为，因为平面PAD与平面ABCD垂直，所以,所以球的半径为，所以求得表面积为。

考查方向

本题考查球的表面积的计算，同时考查了学生的空间想象能力。

解题思路

本题考查球的表面积的计算,关键是找出球心所在的位置并求出球的半径,本题利用了补体的思想,将棱锥补成棱柱,借助棱柱来寻找球心的位置.。

易错点

本题容易因为找不到球心的位置而导致题目不会做。

知识点

棱锥的结构特征

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点