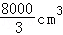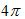- 立体几何与空间向量
- 共2637题
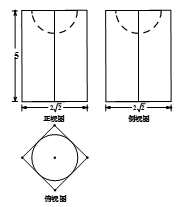
某路口的机动车隔离墩的三视图如右图所示，其中正视图、侧视图都是由半圆和矩形组成，根据图中标出的尺寸（单位：cm）可求得隔离墩的体积为______
正确答案
解析
略
知识点
已知矩形ABCD的顶点都在半径为5的球O的球面上，且
正确答案
解析
略
知识点
.如图2，某简单几何体的正（主）视图与侧（左）视图都是边长为1的正方形，且其体积为
A
B
C
D
正确答案
解析
知识点
具有如图所示的正视图和俯视图的几何体中，体积最大的几何体的表面积为
A3
B7+3
C
D14
正确答案
解析
略
知识点
在
（1）求角
（2）求
正确答案
见解析。
解析
知识点
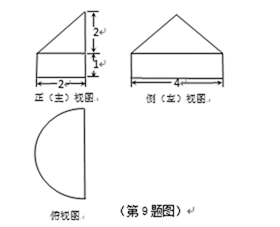
某几何体的三视图如图所示，则它的体积是（ ）。
A
B
C
D
正确答案
解析
由三视图可知，该组合体（如图）下面是边长为
所以组合体的体积为
知识点
若某空间几何体的三视图如图所示，则该几何体的体积是（ ）。
A
B
C
D
正确答案
解析
略
知识点
某几何体的三视图如图所示，其俯视图是由一个半圆与其直径组成的图形，则此几何体的体积是
A
B
C
D
正确答案
解析
略
知识点
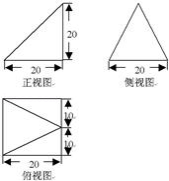
已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是 。
正确答案
解析
先有三视图得到几何体的形状及度量关系，利用棱锥的体积公式求出体积。
解：由三视图可得几何体是四棱锥V﹣ABCD，
其中面VCD⊥面ABCD；
底面ABCD是边长为20cm的正方形；棱锥的高是20cm
由棱锥的体积公式得V=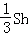
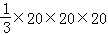
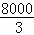
知识点
如图，
正确答案
解析
略
知识点
如图为某几何体的三视图，则其侧面积为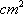 
正确答案
解析
略
知识点
在平面斜坐标系
A
B
C
D
正确答案
解析
略
知识点
非零向量
A
B
C
D以上均不对
正确答案
解析
略
知识点
已知某几何体的三视图如图4所示，则该几何体的表面积和体积分别为 ▲ 与 ▲ .
正确答案
解析
由三视图可知，几何体是底部是一底面对角线长为
球的表面积和体积分别为
故几何体的表面积为
几何体的体积为
知识点
设正四面体
正确答案
解析
略
知识点
扫码查看完整答案与解析