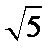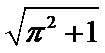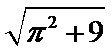立体几何与空间向量_章节学习

1

题型：填空题

|

填空题 · 5 分

12.已知圆锥的侧面展开图是一个半径为3，圆心角为的扇形，则此圆锥的体积为________.

正确答案

解析

∵圆锥侧面展开图是一个圆心角为120°半径为3的扇形∴圆锥的母线长为=3，底面周长即扇

形的弧长为，∴底面圆的半径r=1，可得底面圆的面积为π×r2=π，又圆锥的高

故圆锥的体积为V=

考查方向

本题主要考查了旋转体（圆柱、圆锥、圆台）

解题思路

由于圆锥侧面展开图是一个圆心角为，半径为3的扇形，可知圆锥的母线长，底面周长即扇形的弧长，由此可以求同底面的半径r，求出底面圆的面积，再由求出圆锥的高，然后代入圆锥的体积公式求出体积．

易错点

本题必须注意圆锥侧面展开图是一个圆心角120°半径为3的扇形

知识点

旋转体（圆柱、圆锥、圆台）

1

题型：单选题

|

单选题 · 5 分

12.一矩形的一边在轴上，另两个顶点在函数的图像上，如图，则此矩形绕轴旋转而成的几何体的体积的最大值是（）

A

B

C

D

正确答案

A

解析

设矩形与函数的交点分别为由题意得：

矩形绕轴旋转而成的几何体为圆柱，其体积为，当且仅当即时取等号，所以矩形绕轴旋转而成的几何体的体积的最大值是。

考查方向

本题主要考查旋转体的体积和基本不等式等知识，意在考查考生的转化与化归能力和综合解决问题的能力。

解题思路

1.先根据题意确定，然后建立体积函数；2.将体积函数变形后利用基本不等式求出其最大值。

易错点

对于函数的最值不会求解；看不出之间的关系导致无从下手。

知识点

函数模型的选择与应用旋转体（圆柱、圆锥、圆台）

1

题型：单选题

|

单选题 · 5 分

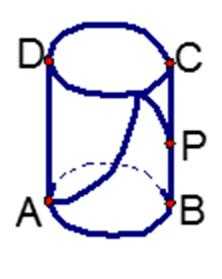
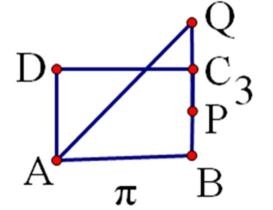
11. 如图，有一圆柱开口容器（下表面封闭），其轴截面是边长为2的正方形，P是BC的中点，现有一只蚂蚁位于外壁A处，内壁P处有一粒米，则这只蚂蚁取得米粒的所经过的最短路程是（）

A;

B

C ;

D

正确答案

D

解析

如图，展开后作辅助线，使得QC=CP,则AQ即为所求最小距离，利用勾股定理可得D选项是正确的。

考查方向

本题主要考查了立体图形的展开问题。

解题思路

将图像展开之后，通过等价转化，最后变成两点间的距离来求解。

易错点

不知道怎样将圆柱展开。。

知识点

旋转体（圆柱、圆锥、圆台）

1

题型：单选题

|

单选题 · 5 分

如图，网格纸上正方形小格的边长为1（表示1cm），图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm，高为6cm的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（　　）

A

B

C

D

正确答案

C

解析

几何体是由两个圆柱组成，一个是底面半径为3高为2，一个是底面半径为2，高为4，

组合体体积是：32π•2+22π•4=34π，底面半径为3cm，高为6cm的圆柱体毛坯的体积为：32π×6=54π。

切削掉部分的体积与原来毛坯体积的比值为：=

知识点

简单组合体的结构特征简单空间图形的三视图棱柱、棱锥、棱台的体积

1

题型：单选题

|

单选题 · 5 分

某几何体的三视图如下图，则几何体的体积为（）

A12

B18

C24

D30

正确答案

C

解析

在长方体中构造几何体,如右图所示，

，经检验该几何体的三视图满足

题设条件。其体积，选择

知识点

组合几何体的面积、体积问题简单空间图形的三视图

1

题型：单选题

|

单选题 · 5 分

在如图所示的空间直角坐标系O﹣xyz中，一个四面体的顶点坐标分别为（0，0，2），（2，2，0），（1，2，1），（2，2，2），给出的编号为①，②，③，④的四个图，则该四面体的正视图和俯视图分别为（　　）

A①和②

B③和①

C④和③

D④和②

正确答案

D

解析

在坐标系中，标出已知的四个点，根据三视图的画图规则，可得三棱锥的正视图和俯视图分别为④②

知识点

简单空间图形的三视图空间直角坐标系

1

题型：单选题

|

单选题 · 5 分

某三棱锥的侧视图、俯视图如图所示，则该三棱锥的体积是（锥体体积公式：，其中S为底面面积，h为高）(　　)

A3

B2

C

D1

正确答案

D

解析

由俯视图知该三棱锥的底面积，由侧视图知该三棱锥的高.

所以，故选D.

知识点

简单空间图形的三视图棱柱、棱锥、棱台的体积

1

题型：填空题

|

填空题 · 5 分

8．圆锥的侧面展开图是圆心角为π，面积为2π的扇形，则圆锥的体积是___________

正确答案

解析

2πr=πl, 2π=πrl.得：r=,l=2,h=1.V=π

考查方向

本题主要考查了圆锥侧面积及体积的运算公式。

解题思路

本题考查运用圆锥侧面积求底面半径及母线，再求高，进而求体积。解题步骤如下：2πr=πl, 2π=πrl.得：r=,l=2,h=1.V=π

易错点

本题必须注意审题，忽视则会出现错误。

知识点

旋转体（圆柱、圆锥、圆台）

1

题型：填空题

|

填空题 · 5 分

13.将边长为2的等边三角形以其一边为轴旋转一周，则形成的几何体的表面积是。

正确答案

4√3π

解析

试题分析：本题属于复数的运算问题，题目的难度较小。注意共轭复数即可。

考查方向

本题主要考查了旋转体的表面积。

解题思路

本题考查旋转体的表面积，解题步骤如下：

旋转体为2个等大的圆锥，高为1，母线长为2，底面半径为√3，所以S=4√3π。

易错点

本题必须注意扇形面积公式，忽视则会出现错误。

知识点

旋转体（圆柱、圆锥、圆台）

1

题型：单选题

|

单选题 · 5 分

6.《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺，问”积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有（）

A14斛

B22斛

C36斛

D66斛

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

旋转体（圆柱、圆锥、圆台）

1

题型：填空题

|

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1

题型：单选题

|

单选题 · 5 分

设图１是某几何体的三视图，则该几何体的体积为

A

B

C

D

正确答案

D

解析

有三视图可知该几何体是一个长方体和球构成的组合体，其体积。

知识点

简单空间图形的三视图棱柱、棱锥、棱台的体积

1

题型：单选题

|

单选题 · 5 分

下图是长和宽分别相等的两个矩形，给定下列三个命题：①存在三棱柱，其正(主)视图、俯视图如下图；②存在四棱柱，其正(主)视图、俯视图如下图；③存在圆柱，其正(主)视图、俯视图如下图，其中真命题的个数是

A3

B2

C1

D0

正确答案

A

解析

对于①,可以是放倒的三棱柱；容易判断②③可以.

知识点

简单空间图形的三视图

1

题型：填空题

|

填空题 · 5 分

一个几何体的三视图如图所示，则该几何体的体积为__________。

正确答案

12＋π

解析

如图所示，由已知得该几何体为一组合体，上面是底面圆半径为1，高为1的圆柱，下面是长为4，宽为3，高为1的长方体，如图所示。

故所求体积V＝π×12×1＋4×3×1＝12＋π。

知识点

简单空间图形的三视图棱柱、棱锥、棱台的体积

1

题型：单选题

|

单选题 · 5 分

一个几何体的三视图如图所示，则该几何体可以是(　　)。

A棱柱

B棱台

C圆柱

D圆台

正确答案

D

解析

从俯视图可看出该几何体上下底面为半径不等的圆，正视图与侧视图为等腰梯形，故此几何体为圆台。

知识点

简单空间图形的三视图

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点