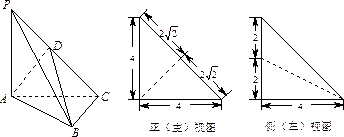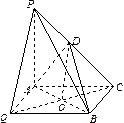- 立体几何与空间向量
- 共2637题
如图，一个空间几何体的正视图、侧视图都是面积为
A
B
C4
D8
正确答案
解析
略
知识点
一个几何体的三视图是三个边长为1的正方形和对角线，如图所示，则此几何体的体积为（ ）
A
B
C
D1
正确答案
解析
由三视图还原原几何体如图，
该几何体是棱长为1的正方体去掉一个棱角，
所以该几何体的体积为
故选C。
知识点
如图，在三棱锥
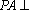
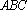
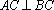
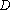
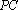
（1）证明：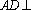
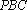
（2）求三棱锥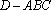
（3）在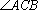
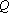
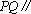
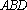
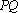
正确答案
见解析。
解析
（1）因为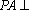
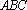
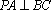
又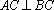
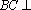
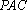
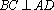
由三视图可得，在
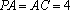
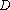
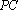
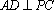
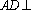
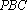
（2）由三视图可得
由⑴知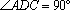
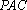
又三棱锥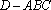
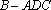
所以，所求三棱锥的体积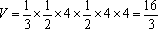
（3）取
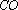
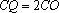
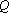
因为
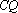
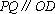
因为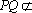
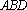
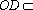
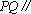
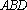
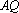
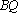
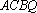
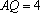
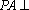
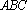
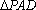
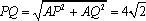
知识点
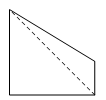
某几何体的直观图如图所示，该几何体的正视图和侧视图可能正确的是（ ）
A
B
C
D
正确答案
解析
略
知识点
下列四个几何体中，各几何体的三视图有且仅有两个视图相同的是
正确答案
解析
①的三个视图都相同：②的主视图与左视图相同，与俯视图不同；③的三个视图互不相同；④的主视图与左视图相同，而与俯视图不同.
知识点
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（ ）
A
B
C
D
正确答案
解析
略
知识点
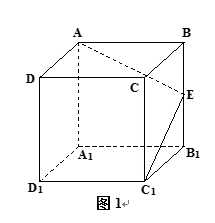
正方体ABCD－A1B1C1D1中，E为棱BB1的中点（如图1），用过点A，E，C1的平面截去该正方体的上半部分，则剩余几何体的左视图为
A
B
C
D
正确答案
解析
取DD1的中点F，连接AF、FC1,则过点A，E，C1的平面即面AEC1F，所以剩余几何体的左视图应为选项C。
知识点
20．在直三棱柱
（1）画出此三棱柱的左视图和俯视图；
（2）求三棱锥
正确答案
（1）左视图为正方形
俯视图为直角三角形
（2）
可得：
解析
解析已在路上飞奔，马上就到！
知识点
7.如图是一个多面体的三视图，则其全面积为（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6． 一个组合体的主视图和左视图相同，如图，其体积为
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10. 一个棱锥的三视图如图，则该棱锥的全面积为（ ）
A36+12
B48+24
C
D36+24
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2．点M、N分别是正方体ABCD
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17．如图，某几何体的正视图与侧视图都是边长为1的正方形，且体积为
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．某三棱锥的三视图如上图所示，该三棱锥的体积是（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9.如图，某几何体的正视图、侧视图和俯视图分别是等边三角形、等腰三角形和菱形，则该几何体的体积为 （ ）
A2
B4
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析