等比数列的判断与证明_章节学习

1

题型：单选题

|

单选题 · 5 分

7.已知，则（）

Ab

Ba < b

Cb

Dc

正确答案

A

知识点

等比数列的判断与证明

1

题型：简答题

|

简答题 · 12 分

已知数列{an}的首项为1， Sn为数列{an}的前n项和，Sn+1=qSn+1，其中q﹥0，n∈N+

23.若a2，a3，a2+a3成等差数列，求数列{an}的通项公式；

24.设双曲线x2﹣=1的离心率为en，且e2=2，求e12+ e22+…+en2，

第(1)小题正确答案及相关解析

正确答案

（Ⅰ）；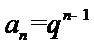

解析

（Ⅰ）由已知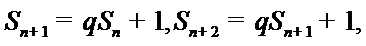，两式相减得到.

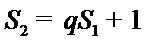
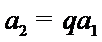
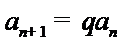
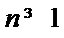
又由得到，故对所有都成立.

所以，数列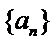是首项为1，公比为q的等比数列.[来源:学.科.网]

从而.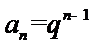

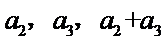
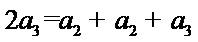
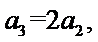
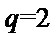
由成等差数列，可得，所以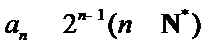，故.

所以.

考查方向

本题考查了数列的通项公式、双曲线的离心率、等比数列的求和公式的知识点

解题思路

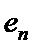
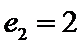
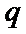
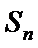
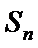
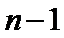
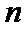
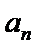
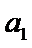
先利用双曲线的离心率定义得到的表达式，再由解出的值，最后利用等比数列的求和公式求解计算.本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识，考查学生的分析问题解决问题的能力、计算能力.在第（Ⅰ）问中，已知的是的递推式，在与的关系式中，经常用代换（），然后两式相减，可得的递推式，利用这种方法解题时要注意；

易错点

本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识，在求离心率时易错。

第(2)小题正确答案及相关解析

正确答案

(Ⅱ).

解析

（Ⅱ）由题意可得，

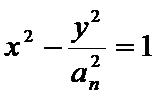
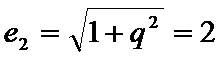
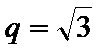
所以双曲线的离心率为

解得.所以

考查方向

本题考查了数列的通项公式、双曲线的离心率、等比数列的求和公式的知识点

解题思路

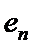
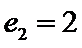
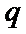
先利用双曲线的离心率定义得到的表达式，再由解出的值，最后利用等比数列的求和公式求解计算.本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识，考查学生的分析问题解决问题的能力、计算能力.在第（Ⅱ）问中，按题意步步为营，认真计算．不需要多少解题技巧，符合文科生的特点．

易错点

本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识，在求离心率时易错。

1

题型：填空题

|

填空题 · 5 分

9.已知等比数列满足,,则（）

正确答案

C

解析

由题意可得 ,所以 ,故 ,选C.

考查方向

本题主要考查等比数列性质及基本运算，属于基础题目.

解题思路

解决本题的关键是利用等比数列性质得到一个关于的一元二次方程,再通过解方程求的值,我们知道,等差、等比数列各有五个基本量,两组基本公式,而这两组公式可看作多元方程,利用这些方程可将等差、等比数列中的运算问题转化解关于基本量的方程（组）,因此可以说数列中的绝大部分运算题可看作方程应用题,所以用方程思想解决数列问题是一种行之有效的方法.

易错点

等比数列性质的灵活应用

知识点

等比数列的判断与证明

1

题型：简答题

|

简答题 · 13 分

已知是等比数列，前n项和为，且.

22.求的通项公式；

23.若对任意的是和的等差中项，求数列的前2n项和.

第(1)小题正确答案及相关解析

正确答案

（Ⅰ）

解析

试题分析：本题属于数列的性质及数列求和的综合应用问题，属于简单题，分组转化法求和的常见类型(1)若an＝bn±cn，且{bn}，{cn}为等差或等比数列，可采用分组求和法求{an}的前n项和．

(2)通项公式为an＝的数列，其中数列{bn}，{cn}是等比数列或等差数列，可采用分组求和法求和．本题只要掌握相关的知识，即可解决本题，解析如下：

试题解析：（Ⅰ）解：设数列的公比为，由已知有，解之可得，又由知，所以，解之得，所以.

考查方向

本题考查了等比数列的通项公式及其前n项和公式等知识点，考察数列求和的基本方法和运算能力。

解题思路

（1）根据已知条件即可求出通项公式；

易错点

正确答案

（Ⅱ）

解析

试题分析：本题属于数列的性质及数列求和的综合应用问题，属于简单题，分组转化法求和的常见类型(1)若an＝bn±cn，且{bn}，{cn}为等差或等比数列，可采用分组求和法求{an}的前n项和．

(2)通项公式为an＝的数列，其中数列{bn}，{cn}是等比数列或等差数列，可采用分组求和法求和．本题只要掌握相关的知识，即可解决本题，解析如下：

（Ⅱ）解：由题意得，即数列是首项为，公差为的等差数列.

设数列的前项和为，则

考查方向

本题考查了等比数列的通项公式及其前n项和公式等知识点，考察数列求和的基本方法和运算能力。

解题思路

（2）先根据等差中项的概念求出数列的通项公式，再利用分组求和法求和．

易错点

正确答案

；

解析

，．

考查方向

方差

解题思路

根据方差公式求解

易错点

公式中要除以n。

知识点

等比数列的判断与证明

1

题型：单选题

|

单选题 · 5 分

4.设，则（）

A

B

C

D

正确答案

C

解析

因为，所以，

故答案选.

考查方向

本题考查函数值的求法，是中档题，解题时要认真审题，注意分段函数的性质的合理运用．

解题思路

本题考查分段函数和复合函数求值，此题需要先求的值，继而去求的值；.若求函数的值，需要先求的值，再去求的值；若是解方程的根，则需先令，即，再解方程求出的值，最后在解方程；属于基础题.

易错点

注意运算的准确性.

知识点

等比数列的判断与证明

1

题型：填空题

|

填空题 · 5 分

14．已知{}为等差数列，公差为1，且a5是a3与a11的等比中项，则a1＝_________．

正确答案

-1

解析

考查方向

本题考察了等差数列的通项公式和等比中项，比较简单

解题思路

1）使用等差数列通项公式使用a1和d表示a5，a3，a11

2）使用等比中项公式得到关系式计算得出a1

易错点

主要易错于计算出错

知识点

等差数列的性质及应用等比数列的判断与证明

1

题型：填空题

|

填空题 · 5 分

11. 在等比数列中，成等差数列，则_____________．

正确答案

3

解析

由题可知，a5=3a1+2a3，q4=3+2q2，q2=3，则q2=3.

考查方向

本题主要考查等比数列的知识

解题思路

表示等差数列，表示首项与公比的关系，代入即可得到结果。

易错点

本题易在表示等差数列时发生错误。

知识点

等比数列的判断与证明

1

题型：简答题

|

简答题 · 16 分

19. 设数列的前项和，，，且当时，．

（1）求证:数列是等比数列，并求数列的通项公式；

（2）令，记数列的前项和为．设是整数，问是否存在正整数，使等式成立？若存在，求出和相应的值；若不存在，说明理由．

正确答案

见解析

解析

解：（1）当时, ,,

代入并化简得,

而恒为正值,∴

∴数列是等比数列.

∴.当时,,

又，∴

（2）当时，,此时，又

∴.

故，

当时，

，

若，

则等式为，不是整数，不符合题意；

若，则等式为，

∵是整数, ∴必是的因数, ∵时

∴当且仅当时，是整数，从而是整数符合题意.

综上可知，当时，存在正整数，使等式成立，

当时，不存在正整数使等式成立.

考查方向

本题考查了等比数列的证明及数列的通项公式求法

解题思路

利用，得数列是等比数列.

易错点

忽略n的范围的讨论。

知识点

由an与Sn的关系求通项an等比数列的判断与证明裂项相消法求和数列与函数的综合

1

题型：简答题

|

简答题 · 12 分

18．在数列{an}中，a1=2，an+1= ，n∈N*.

(1)求证：是等比数列；

(2)求数列{an}的前n项之和Sn．

正确答案

略．

解析

试题分析：本题属于数列中的基本问题，题目的难度是逐渐由易到难．

（1）由已知得。

所以是以1为首项，2为公比的等比数列。

考查方向

本题考查了数列的问题．属于高考中的高频考点。

解题思路

本题考查数列问题，解题步骤如下：

（1）利用等比数列的定义证明。

（2）利用错位相减法求和。

易错点

错位相减法求和时相减的结果项数易错。

知识点

等比数列的判断与证明错位相减法求和

热门试卷

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点