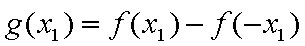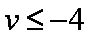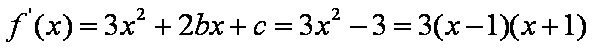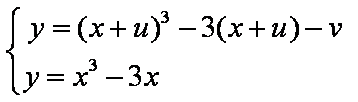- 利用导数研究函数的单调性
- 共252题
已知函数


(1)求

(2)对函数



正确答案
见解析
解析
解析:
(1)由
而点


又直线
故有
(2)由(1)得
由

令
令
故

故当

当
从而当





故
要使



知识点
已知函数f(x)=(3x2-6X+6)ex-x3
(1)求函数f(x)的单调区间及极值;
(2)若 x1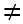
正确答案
见解析。
解析
(1)∵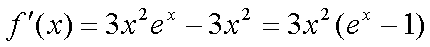
∴当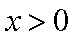
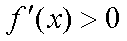
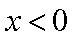
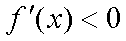
则
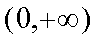
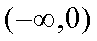
所以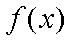
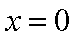
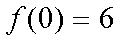
(2)∵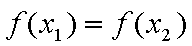
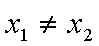
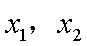
不妨设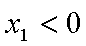

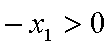
令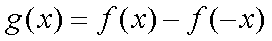
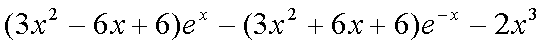
则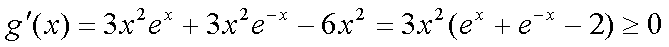
所以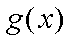
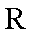
又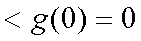
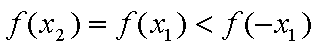
又∵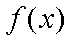
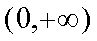
∴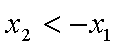

知识点
已知函数
(1)若

(2)若


正确答案
见解析
解析
(1)当













(2)由







令




∴
即


知识点
设二次函数






正确答案
解析
略
知识点
已知函数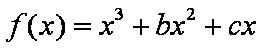
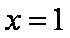
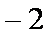
(1)求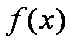
(2)若对任意的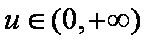
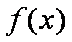
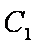

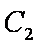
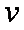
正确答案
(1)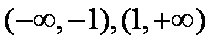
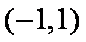
(2)
解析
(1)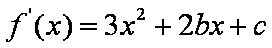
由题意得: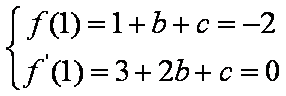
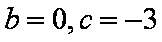
∴
∴当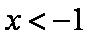
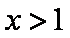

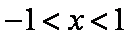
∴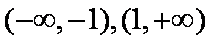
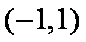
(2)
由方程组
得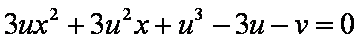
∴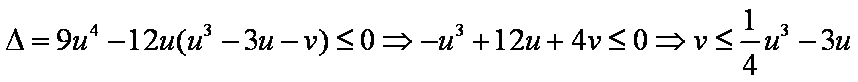
……………………………………9 分
令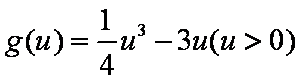
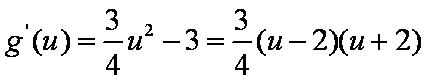
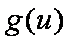
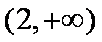
所以当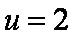
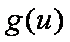
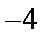
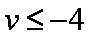
知识点
扫码查看完整答案与解析