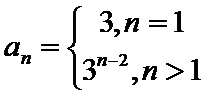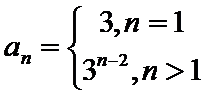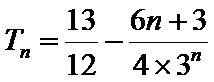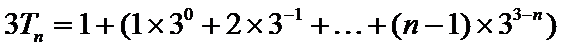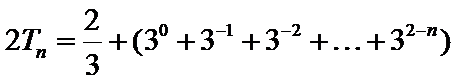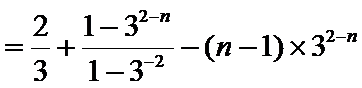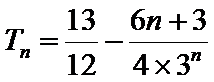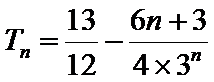等比数列的判断与证明
共122题

· 等比数列的判断与证明

等比数列的判断与证明
共122题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

设数列{an}的前n项和为Sn，已知2Sn=3n+3．

20.求{an}的通项公式；

21.若数列{bn}，满足anbn=log3an，求{bn}的前n项和Tn．

第(1)小题正确答案及相关解析

正确答案

（1）

解析

（I）因为，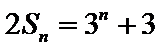

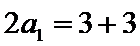
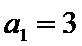
所以，故，

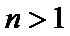
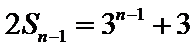
当时，，

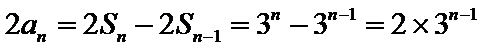
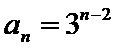
此时，即，

所以

考查方向

考查等差数列的通项公式的求法

解题思路

运用从一般到特殊的处理方法，准确确定等差数列的通项公式。

（Ⅰ）利用2Sn=3n+3，可求得a1=3；当n＞1时，2Sn﹣1=3n﹣1+3，两式相减2an=2Sn﹣2Sn﹣1，可求得an=3n﹣1，从而可得{an}的通项公式。

第(2)小题正确答案及相关解析

正确答案

（2）

解析

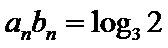
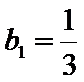
（II）因为，所以，

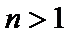
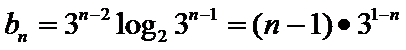
当时，，

所以；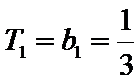

，

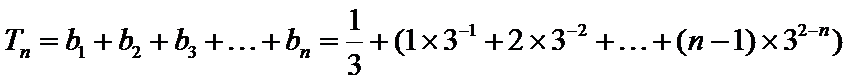
所以

两式相减，得

，

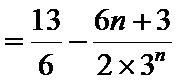
所以

经检验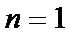，也适合，

综上可得

考查方向

本题考查数列的求和，着重考查数列递推关系的应用，突出考“查错位相减法”求和，考查分析、运算能力，属于中档题．

解题思路

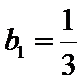
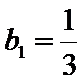
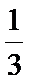
（Ⅱ）依题意，anbn=log3an，可得，当n＞1时，bn=31﹣n•log33n﹣1=（n﹣1）×31﹣n，于是可求得T1=；当n＞1时，Tn=b1+b2+…+bn=+（1×3﹣1+2×3﹣2+…+（n﹣1）×31﹣n），利用错位相减法可求得{bn}的前n项和Tn．

易错点

数列的错位相减求和时错项的处理，等差数列与等比数列的性质．

题型：单选题

单选题 · 5 分

4.已知数列的前项和为，且a1=2，a2=3，Sn为数列的前n项和，则S2016的值为（）

正确答案

解析

因为, a1=2，a2=3，所以a3=1,a4=-2,a5=-3,a6=-1,a7=2,……可知每6项循环一次，且和为0,所以2016/6=336，所以和为0.

考查方向

数列求和

解题思路

先写出前几项，然后找到规律，进而求解

易错点

找不出前n项和和数列通项的关系

知识点

等比数列的判断与证明

题型：单选题

单选题 · 5 分

2．设{an}是公比为q的等比数列，则“q>1”是“{an}为递增数列”的(　　)

A充分而不必要条件

B必要而不充分条件

C充分必要条件

D既不充分也不必要条件

正确答案

解析

根据指数函数的单调性，举反例：首项时，q=2，{an}是递减数列；反之，{an}为递增数列，q>1也不正确，如： ,0<q<1. 所以选D

考查方向

本题考查等比数列的单调性，充分条件与必要条件.

解题思路

等比数列的增减是由首项与公比确定的，当首项时，q>1，{an}是递减数列；反之，{an}为递增数列，q>1也不正确，如： ,0<q<1

易错点

对递增等比数列判断不准，对条件的性质判断不准.

知识点

等比数列的判断与证明等比数列的性质及应用

题型：填空题

填空题 · 6 分

11.设等比数列的前项和为，已知，某同学经过计算得到检验后发现其中恰好一个数算错了，则算错的这个数是　 ▲ ，该数列的公比是　 ▲ ．

正确答案

32（），.

解析

根据题意依次算出等比数列的前四项，分别为16，-16，-44，-54，若,则q=1,这与54矛盾，所以是错误的，所以该组数据中出错的是，所以,54=16，q=

考查方向

本题主要考查等比数列的前n项和及通项公式;逻辑推理能力.

解题思路

根据题意依次算出等比数列的前四项，分别为16，16，44，54，可判断出第二项不可能是16，所以该组数据中出错的是 , 再根据第四项计算出等比数列的公比.

易错点

本题易在“检验后发现其中恰好一个数算错了” 这句话理解上出错.

知识点

等比数列的判断与证明等比数列的性质及应用

题型：简答题

简答题 · 12 分

已知单调递增的等比数列满足：且是的等差中项．

17.求数列的通项公式；

18.若，其前项和为，求．

第(1)小题正确答案及相关解析

正确答案

由得，

由且为递增数列，解得，

故，则

第(2)小题正确答案及相关解析

正确答案

继续学习学习下一知识点

下一知识点 : 等比数列的性质及应用

百度题库 > 高考 > 理科数学 > 等比数列的判断与证明

扫码查看完整答案与解析