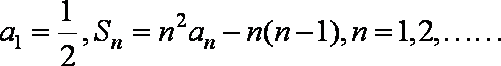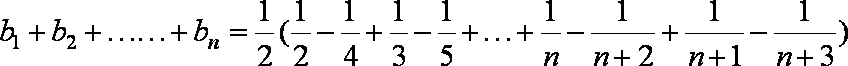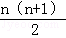- 等比数列的判断与证明
- 共122题
已知数列






(1)求证:数列
(2)求数列


正确答案
见解析。
解析
(1)由已知可得,



(2)


① - ② 得


∴
知识点
已知数列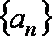
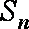
(1)证明:数列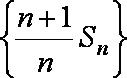
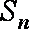
(2)设
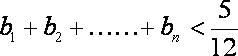
正确答案
见解析
解析
证明:(1)由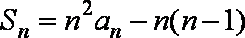
当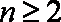
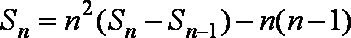
即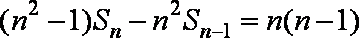
∴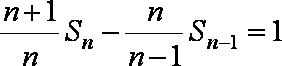
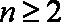
又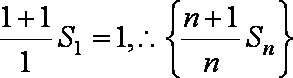

∴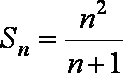
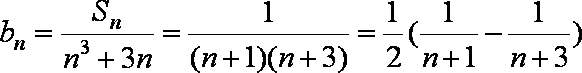
∴
=
知识点
已知数列{an}的前n项和为Sn,且
(1)证明:数列{3+an}是等比数列,并求出数列{an}的通项公式;
(2)设bn=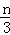
(3)数列{an}中是否存在构成等差数列的四项?若存在求出一组;否则说明理由。
正确答案
见解析。
解析
(1)由an=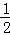
由待定系数法得an+1+3=2(an+3)又a1+3=6≠0
∴数列{an+3}是以6为首项,2为公比的等比数列。
∴an+3=6×2n﹣1,
∴an=3(2n﹣1),
(2)由(1)可得bn=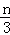
∴Bn=1×21+2×22+3×23+…+n×2n﹣(1+2+3+…+n) ①
∴2Bn=1×22+2×23+3×24+…+n×2n+1﹣2(1+2+3+…+n) ②
①﹣②得,﹣Bn=2+(22+23+…+2n)+
化简可得Bn=2+
(3)假设数列{an}存在构成等差数列的四项依次为:am、an、ap、aq(m<n<p<q)
则3(2m﹣1)+3(2q﹣1)=3(2n﹣1)+3(2p﹣1)∴2m+2q=2n+2p。
上式两边同除以2m,则1+2q﹣m=2n﹣m+2p﹣m
∵m、n、p、q∈N*,且m<n<p<q,∴上式左边是奇数,右边是偶数,相矛盾。
∴数列{an}不存在构成等差数列的四项。
知识点
已知数列



(1)求

(2)设
(i)求
(ii)令



正确答案
(1)


解析
解析:(1)由
由

(2)(i)

(ii)


① - ②得


知识点
数列



(1)求数列

(2)设



正确答案
见解析
解析
(1)

则


则
(2)
则
两式相减得
整理得
知识点
扫码查看完整答案与解析