- 等比数列的判断与证明
- 共122题
设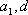
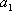
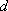
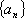


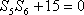
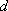
正确答案
(-∞,-2

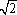
解析
2a12+9a1d+10d2+1=0,此方程有解,所以△=81d2-8(10d2+1)>0,得d>2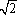
知识点
已知等比数列

正确答案
解析
等比数列





知识点
已知数列



(1)若



(2)证明:数列




正确答案
见解析
解析
(1)对任意

即

(2)①必要性:若数列




即




②充分性:若对于任意


则
于是
即
由



因为




综上所述,数列



知识点
设等比数列




(1)求数列
(2)在




求证:

正确答案
见解析。
解析
(1)设等比数列






即

当


即
(2)①

设

① -②得:
=
知识点
设{an}是公比为q的等比数列。
(1)推导{an}的前n项和公式;
(2)设q≠1,证明数列{an+1}不是等比数列。
正确答案
见解析
解析
(1)设{an}的前n项和为Sn,
当q=1时,Sn=a1+a1+…+a1=na1;
当q≠1时,Sn=a1+a1q+a1q2+…+a1qn-1,①
qSn=a1q+a1q2+…+a1qn,②
①-②得,(1-q)Sn=a1-a1qn,
∴
(2)证明:假设{an+1}是等比数列,则对任意的k∈N+,
(ak+1+1)2=(ak+1)(ak+2+1),

a12q2k+2a1qk=a1qk-1·a1qk+1+a1qk-1+a1qk+1,
∵a1≠0,∴2qk=qk-1+qk+1.
∵q≠0,∴q2-2q+1=0,
∴q=1,这与已知矛盾,
∴假设不成立,故{an+1}不是等比数列
知识点
扫码查看完整答案与解析