- 二次函数在闭区间上的最值
- 共37题
函数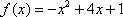
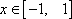
正确答案
4
解析
略
知识点
二次函数

正确答案
解析





知识点
已知


(1)求

(2)当


正确答案
见解析。
解析
(1)
当



当



当



(2) 当






①



而



显然










②





综上所述,
知识点
已知命题



① 命题“

③ 命题“

其中正确的是 ( )
正确答案
解析
略
知识点
已知函数


⑴


⑵若函数

正确答案
见解析。
解析
(1)









(2)



依题意,








设


综上所述,常数
知识点
扫码查看完整答案与解析












