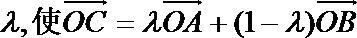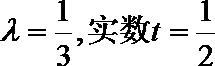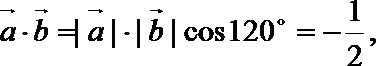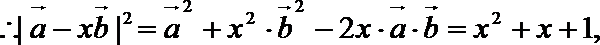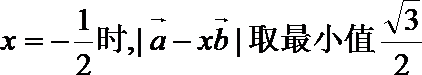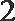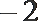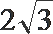- 数量积表示两个向量的夹角
- 共77题
已知正三角形ABC中,D是BC的中点,AB=3,BD=1,则
正确答案
解析
知识点
已知椭圆



(1)求椭圆标准方程;
(2)若直线










(3)若点







正确答案
见解析。
解析
(1)有题设可知:

又

∴椭圆标准方程为
(2)设P(x,y),A(x1,y1),B(x2,y2),
则由
(x,y)=(x1,y1)+


即x=x1+

因为点A、B在椭圆x2+2y2=2上,
所以x+2y=2,x+2y=2,(6分)
故x2+2y2=(x+



=(x+2y)+

=2+2

设kOA,kOB分别为直线OA,OB的斜率,
由题设条件知kOA·kOB=

因此x1x2+2y1y2=0,
所以x2+2y2=2+2

所以P点是椭圆
设该椭圆的左、右焦点为F1,F2,
则由椭圆的定义|PF1|+|PF2|为定值。
又因c=
因此两焦点的坐标为F1(-

所以存在两个定点F1(-

(8分)
(Ⅲ)设
由题意可知:



将③代入④可得:
点A,D在椭圆x2+2y2=2上,
∴
∴

知识点
设A、P是椭圆
正确答案
解析
不妨设点P是椭圆的右顶点,即P


知识点
已知平面向量



正确答案
答案:
解析
略
知识点
14.已知向量






正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
18.设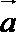
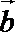
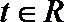
(1)记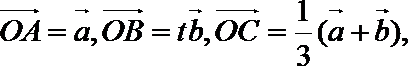
(2)若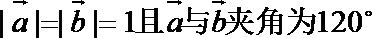
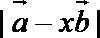
正确答案
解:(1)A、B、C三点共线知存在实数
即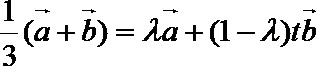
则
(2)
当
解析
解析已在路上飞奔,马上就到!
知识点
19.已知:向量




(1)若


(2)若



正确答案
(1)∵

①若





②若





(2)∵

∴ 


∴|






∴
解析
解析已在路上飞奔,马上就到!
知识点
4.已知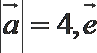
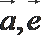
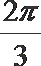
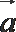
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知向量








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知△ABC中,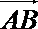
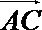
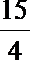
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析