极坐标刻画点的位置
共11题

· 极坐标刻画点的位置

极坐标刻画点的位置
共11题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 10 分

22.选修4-4：坐标系与参数方程

在极坐标系中，已知圆的圆心，半径.

（Ⅰ）求圆的极坐标方程；

（Ⅱ）若点在圆上运动，点在的延长线上，且||∶||＝，求动点的轨迹方程．

正确答案

（1）；

（2）．

解析

试题分析：本题属于坐标系与参数方程中的基本问题，题目的难度一般，解题过程如下：

（Ⅰ）设为圆上任一点，的中点为，

∵在圆上，∴为等腰三角形，由垂径定理可得

∴即为所求圆的极坐标方程．

（Ⅱ）设点的极坐标为，因为在的延长线上，且，所以点的坐标为，由于点在圆上，所以,故点的轨迹方程为。

考查方向

本题考查了坐标系与参数方程的专题知识，考查了极坐标方程的相关知识。

解题思路

本题考查极坐标方程的知识，可以根据求圆的极坐标方程所需的条件寻求关系。

易错点

没有准确理解极坐标下的轨迹方程而导致本题不会做。

知识点

极坐标刻画点的位置

题型：填空题

填空题 · 5 分

（坐标系与参数方程选做题）已知直线的参数方程为：（为参数），圆的极坐标方程为，则圆的圆心到直线的距离为 .

正确答案

解析

略

知识点

极坐标刻画点的位置

题型：填空题

填空题 · 5 分

在极坐标系中，定点，点在直线上运动，当线段最

短时，点的极坐标为，

正确答案

解析

略

知识点

极坐标刻画点的位置

题型：填空题

填空题 · 5 分

在极坐标系中，O为极点，直线过圆C：的圆心C，且与直线OC垂直，则直线的极坐标方程为。

正确答案

（或）；

解析

把化为直角坐标系的方程为，圆心C的坐标为（1，1），与直线OC垂直的直线方程为化为极坐标系的方程为或.

知识点

极坐标刻画点的位置

题型：填空题

填空题 · 5 分

（坐标系与参数方程选做题）在极坐标系中，曲线与的交点的极坐标为________。

正确答案

解析

曲线与分别转化为直角方程得，。联立，解得或（舍去）。∴，，又，∴，∴交点的极坐标为。

另解：联立，解得或（舍去），∴曲线与的交点的极坐标为。

知识点

极坐标刻画点的位置

题型：填空题

填空题 · 5 分

在极坐标系中，直线被圆截得的弦长为

正确答案

解析

将直线与圆的方程化为直角坐标方程分别为：和，显然直线过圆心，故所求的弦长即圆的直径4。

知识点

极坐标刻画点的位置

题型：简答题

简答题 · 10 分

已知曲线C1的参数方程为(t为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ＝2sin θ.

（1）把C1的参数方程化为极坐标方程；

（2）求C1与C2交点的极坐标(ρ≥0,0≤θ＜2π)。

正确答案

（1）ρ2－8ρcos θ－10ρsin θ＋16＝0.

（2），

解析

（1）将消去参数t，化为普通方程(x－4)2＋(y－5)2＝25，

即C1：x2＋y2－8x－10y＋16＝0.

将代入x2＋y2－8x－10y＋16＝0得ρ2－8ρcos θ－10ρsin θ＋16＝0.

所以C1的极坐标方程为

ρ2－8ρcos θ－10ρsin θ＋16＝0.

（2）C2的普通方程为x2＋y2－2y＝0.

由

解得或

所以C1与C2交点的极坐标分别为，.

知识点

简单曲线的极坐标方程极坐标刻画点的位置极坐标系和平面直角坐标的区别圆的参数方程

题型：填空题

填空题 · 5 分

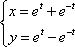
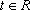
（坐标系与参数方程选做题）曲线C的参数方程为，为参数，, 曲线C的普通方程为。

正确答案

解析

略

知识点

极坐标刻画点的位置

题型：简答题

简答题 · 10 分

已知曲线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

（1）把的参数方程化为极坐标方程；

（2）求与交点的极坐标（.

正确答案

见解析

解析

解析：将消去参数，化为普通方程,

即：.将代入得

（2）的普通方程为.

由，解得或.

所以与交点的极坐标分别为，

知识点

简单曲线的极坐标方程极坐标刻画点的位置参数方程化成普通方程圆的参数方程

题型：填空题

填空题 · 5 分

14．在极坐标系中，点M到曲线上的点的距离的最小值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

极坐标刻画点的位置

继续学习学习下一知识点

下一知识点 : 极坐标系和平面直角坐标的区别

百度题库 > 高考 > 文科数学 > 极坐标刻画点的位置

扫码查看完整答案与解析