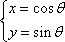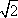选修部分_章节学习

1

题型：填空题

|

填空题 · 5 分

已知曲线的参数方程为（为参数），则曲线的直角坐标方程为（）。

正确答案

解析

略

知识点

参数方程化成普通方程

1

题型：单选题

|

单选题 · 5 分

椭圆（是参数）的离心率是（）。

A

B

C

D

正确答案

B

解析

略

知识点

椭圆的几何性质参数方程化成普通方程椭圆的参数方程

1

题型：填空题

|

填空题 · 5 分

已知是曲线的焦点，，则的值是。

正确答案

解析

略

知识点

抛物线的定义及应用参数方程化成普通方程抛物线的参数方程

1

题型：填空题

|

填空题 · 5 分

在平面直角坐标系中，已知直线C:（是参数）被圆C:截得的弦长为（）

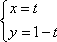
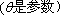
正确答案

解析

略

知识点

直线与圆相交的性质参数方程化成普通方程直线的参数方程圆的参数方程

1

题型：简答题

|

简答题 · 10 分

在直角坐标系中，曲线的参数方程为（为参数），曲线的参数方程为（为参数），是上的点，线段的中点在上。

（1）求和的公共弦长；

（2）在以为极点，轴的正半轴为极轴的极坐标系中，求点的一个极坐标.

正确答案

见解析。

解析

（1）曲线的一般方程为，

曲线的一般方程为。

两圆的公共弦所在直线为，

到该直线距离为，所以公共弦长为。

（2）曲线的极坐标方程为，

曲线的极坐标方程为。

设，则，两点分别代入和解得，

不妨取锐角，

所以。

知识点

圆与圆的位置关系及其判定极坐标刻画点的位置参数方程化成普通方程圆的参数方程

1

题型：填空题

|

填空题 · 5 分

已知函数f（x）=，若关于x的方程f（x）=kx（k＞0）有且仅有四个根，其最大根为t，则函数g（t）=﹣6t+7的值域为　。

正确答案

[﹣，﹣1）　

解析

作出函数f（x）=，当0≤x＜4时的图象，如右图中红色的三个半圆。

将直线y=kx围绕坐标原点进行旋转，可得当直线介于与第二个半圆相切和与第三个半圆相切之间时，两图象有且仅有四个不同的公共点，

此时，其最大根t∈（，），

则函数g（t）=﹣6t+7，t∈（，）的值域为[﹣，﹣1）。

故答案为：[﹣，﹣1）。

知识点

参数方程化成普通方程

1

题型：简答题

|

简答题 · 10 分

已知直线为参数), 曲线（为参数）.

（1）设与相交于两点,求；

（2）若把曲线上各点的横坐标压缩为原来的倍,纵坐标压缩为原来的倍,得到曲线,设点是曲线上的一个动点,求它到直线的距离的最小值。

正确答案

见解析

解析

（1）的普通方程为的普通方程为

联立方程组解得与的交点为,,则.

（2）的参数方程为为参数)。故点的坐标是,

从而点到直线的距离是,

由此当时,取得最小值,且最小值为.

知识点

函数的图象与图象变化直线与圆相交的性质参数方程化成普通方程直线的参数方程圆的参数方程

1

题型：简答题

|

简答题 · 10 分

在直角坐标系中,以原点为极点,轴的正半轴为极轴建坐标系.已知曲线,已知过点的直线的参数方程为：，直线与曲线分别交于两点.

（1）写出曲线和直线的普通方程；

（2）若成等比数列,求的值。

正确答案

见解析

解析

解析：

（1）.

（2）直线的参数方程为（为参数）,

代入, 得到，则有.

因为，所以. 解得

知识点

数列与解析几何的综合点的极坐标和直角坐标的互化参数方程化成普通方程

1

题型：简答题

|

简答题 · 10 分

在直角坐标系中，圆的参数方程为参数），以为极点，轴的非负半轴为极轴建立极坐标系。

（1）求圆的极坐标方程；

（2）直线的极坐标方程是，射线与圆的交点为，与直线的交点为，求线段的长。

正确答案

见解析

解析

（1）圆的普通方程为，又

所以圆的极坐标方程为

（2）设，则有解得

设，则有解得

所以

知识点

直线与圆相交的性质简单曲线的极坐标方程参数方程化成普通方程圆的参数方程

1

题型：简答题

|

简答题 · 10 分

在直角坐标系中，直线l的参数方程为：在以O为极点，以x 轴的正半轴为极轴的极坐标系中，圆C的极坐标方程为：

（1）将直线l的参数方程化为普通方程，圆C的极坐标方程化为直角坐标方程；

（2）判断直线与圆C的位置关系。

正确答案

（1）（2）直线与圆相交

解析

（1）将直线的参数方程经消参可得直线的普通方程为： 3分

由得，

即圆直角坐标方程为.6分

（2）由（1）知，圆的圆心，半径，

则圆心到直线的距离故直线与圆相交。10分

知识点

直线与圆的位置关系简单曲线的极坐标方程点的极坐标和直角坐标的互化参数方程化成普通方程椭圆的参数方程

1

题型：简答题

|

简答题 · 7 分

已知曲线C1：（为参数），曲线C2：（t为参数）。

（1）指出C1，C2各是什么曲线，并说明C1与C2公共点的个数；

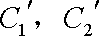
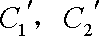
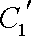
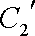
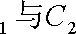
（2）若把C1，C2上各点的纵坐标都压缩为原来的一半，分别得到曲线，写出的参数方程。与公共点的个数和C公共点的个数是否相同？说明你的理由。

正确答案

见解析

解析

（1）是圆，是直线。

的普通方程为，圆心，半径。

的普通方程为。 ……………2分

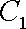
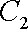
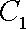
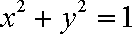
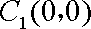
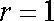
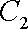
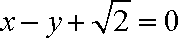
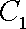
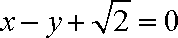
因为圆心到直线的距离为，

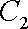
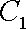
所以与只有一个公共点。 ……………4分

（2）压缩后的参数方程分别为

：（为参数）；：（t为参数）。

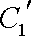
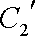
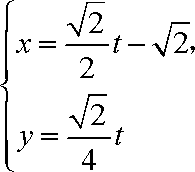
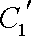
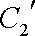
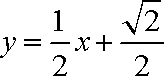
化为普通方程为：：，：，……………6分

联立消元得，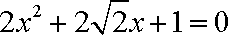

其判别式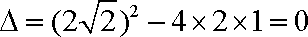，……………7分

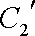
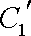
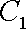
所以压缩后的直线与椭圆仍然只有一个公共点，和与公共点个数相同。

知识点

直线与圆的位置关系参数方程化成普通方程直线的参数方程圆的参数方程

1

题型：简答题

|

简答题 · 10 分

已知极坐标系与直角坐标系长度单位相同，且以原点O为极点， x轴的非负半轴为极轴. 设直线C1： (t为参数)，曲线C2：=1.

（1）当时，求曲线C1的极坐标方程及极径的最小值；

（2）求曲线C1与C2两交点的直角坐标（用表示）。

正确答案

见解析

解析

（1）当时，C1的普通方程为，………………1分

又因为，代入上式得

故曲线C1的极坐标方程为 ……………………3分

当时可得，极径的最小值 ……………5分

（2）消去参数得C1的普通方程为，C 2的普通方程为，……………………7分

二者联立，将代入

得

因为判别式△=4，所以设其二根分别为

，……………………9分

即所求的中点的直角坐标为（，）…………10分

知识点

直线与圆相交的性质简单曲线的极坐标方程参数方程化成普通方程

1

题型：简答题

|

简答题 · 10 分

在极坐标系中，圆，以极点为坐标原点，极轴为x轴正半轴建立平面直角坐标系，设直线的参数方程为为参数）。

（1）求圆C的标准方程和直线的普通方程；

（2）若直线与圆C恒有公共点，求实数的取值范围。

正确答案

见解析

解析

（1）由得

所以直线的普通方程为：，………………………2分

由

又

所以，圆的标准方程为，………………………5分

（2）因为直线与圆恒有公共点，所以，…………7分

两边平方得

所以a的取值范围是.……………………………………………10分

知识点

直线与圆的位置关系点的极坐标和直角坐标的互化参数方程化成普通方程

1

题型：简答题

|

简答题 · 10 分

已知圆的参数方程为（为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，圆的极坐标方程为。

（1）将圆的参数方程化为普通方程，将圆的极坐标方程化为直角坐标方程；

（2）圆、是否相交，若相交，请求出公共弦的长；若不相交，请说明理由。

正确答案

见解析

解析

解析：（1）由得x2＋y2＝1，

又∵ρ＝2cos(θ＋)＝cosθ－sinθ，

∴ρ2＝ρcosθ－ρsinθ.

∴x2＋y2－x＋y＝0，即 ………………5分

（2）圆心距，得两圆相交

由得，A(1,0)，B，

∴ ………………10分

知识点

圆与圆的位置关系及其判定点的极坐标和直角坐标的互化参数方程化成普通方程

1

题型：简答题

|

简答题 · 10 分

已知平面直角坐标系,以为极点, 轴的非负半轴为极轴建立极坐标系, ,曲线的参数方程为.点是曲线上两点，点的极坐标分别为.

（1）写出曲线的普通方程和极坐标方程;

（2）求的值。

正确答案

见解析

解析

解析：（1）参数方程普通方程 ………3分

普通方程 ……………………6分

方法1：可知,为直径，

方法2直角坐标两点间距离……10分

知识点

两点间距离公式的应用简单曲线的极坐标方程参数方程化成普通方程

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点