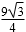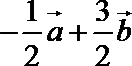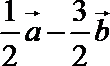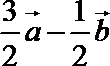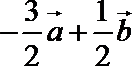- 向量加减混合运算及其几何意义
- 共9题
7.设四边形ABCD为平行四边形，
正确答案
解析
考查方向
解题思路
先将所求向量用题中给出的向量表示出来后代人要求的式子化简即可。
易错点
1.不知道如何将题中要求的向量用已知向量表示；
利用向量的法则表示向量时出错。
知识点
8.如图，在等腰梯形
使得
A（
B（
C（
D（
正确答案
解析
以DC所在直线为x轴，DC的中垂线为y轴建立平面直角坐标系，则梯形的高为
\
考查方向
解题思路
该题使用建立坐标系，设P的坐标，根据
易错点
主要易错于讨论不全，漏解
知识点
14.如图，在
正确答案
解析
由
考查方向
解题思路
1.先将向量
易错点
1.在将BE用向量表示时由于运算出错；2.不会将求BE的长度转化为求向量的模的运算。
知识点
7．已知菱形
A
B
C
D
正确答案
解析
考查方向
解题思路
画出图形，分别把
易错点
不会利用向量加法的几何意义运算或进行向量的数量积运算时，夹角出错，
知识点
7．在
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14．在△ABC中有如下结论：“若点M为△ABC的重心，则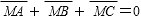
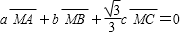
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5.设A1,A2,A3,A4是平面直角坐标系中两两不同的四个点,若
正确答案
解析
根据题意可知
若C或D是线段AB的中点,
则
此时不可能有
若C,D可能同时在线段AB上,
则0<λ<1,0<μ<1,则
若C,D同时在线段AB的延长线上,
则λ>1,μ>1,0
故C,D不可能同时在线段AB的延长线上.
知识点
2.若向量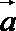
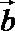
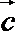
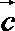
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．如图，在矩形OABC中，点E、F分别在线段AB、BC上，且满足
正确答案
解析
以
设
∵
∴
∵
∴
∴
得
解得
考查方向
本题考查了向量的坐标运算及平面向量分解定理，属于容易题，在近几年的各省高考题出现的频率较高，常与直线、圆锥曲线、数列、函数等知识点交汇命题．
解题思路
用坐标法求解；恰当选择新的基向量，寻找
易错点
题中所选的基向量不垂直，学生不容易找到相互之间的关系．
知识点
扫码查看完整答案与解析