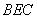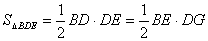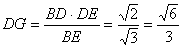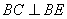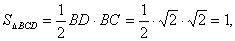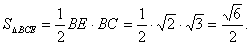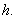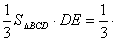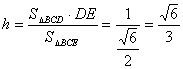- 直线和圆的方程
- 共1163题
设

正确答案
解析
若







知识点
下图是某公司10个销售店某月销售某产品(单位:台)的茎叶图,则数据落在区间
正确答案
解析
∵数据总个数n=10,
又∵落在区间[22,30)内的数据个数为4,
∴所求的频率为
知识点
某市为了考核甲、乙两部门的工作情况,随机访问了50位市民,根据这50位市民对两部门的评分(评分越高表明市民的评价越高)绘制的茎叶图如图:
(1)分别估计该市的市民对甲、乙两部门评分的中位数;
(2)分别估计该市的市民对甲、乙两部门的评分高于90的概率;
(3)根据茎叶图分析该市的市民对甲、乙两部门的评价。
正确答案
见解析。
解析
(1)由茎叶图知,50位市民对甲部门的评分有小到大顺序,排在排在第25,26位的是75,75,故样本的中 位数是75,所以该市的市民对甲部门的评分的中位数的估计值是75。
50位市民对乙部门的评分有小到大顺序,排在排在第25,26位的是66,68,故样本的中位数是
(2)由茎叶图知,50位市民对甲、乙部门的评分高于90的比率分别为
故该市的市民对甲、乙两部门的评分高于90的概率得估计值分别为0.1,0.16,
(3)由茎叶图知,市民对甲部门的评分的中位数高于乙部门的评分的中位数,而且由茎叶图可以大致看出对甲 部门的评分标准差要小于乙部门的标准差,说明该市市民对甲部门的评价较高、评价较为一致,对乙部门 的评价较低、评价差异较大
知识点
要得到函数

正确答案
解析

知识点
设函数f(x)=x2-4x+3,g(x)=3x-2,集合M={x∈R|f(g(x))>0},N={x∈R|g(x)<2},则M∩N为…( )
正确答案
解析
函数f(x)=(x-3)(x-1),令f(x)>0得x>3或x<1,不等式f(g(x))>0可化为g(x)>3或g(x)<1,即3x-2>3或3x-2<1,分别求解得x>log35或x<1,即M={x∈R|x>log35或x<1},N={x∈R|3x-2<2}={x∈R|x<log34},所以M∩N={x∈R|x<1},故选D项
知识点
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
(1)求回归直线方程

(2)预计在今后的销售中,销量与单价仍然服从(Ⅰ)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
正确答案
(1) 
解析
(1)由于



所以a=


(2)设工厂获得的利润为L元,依题意得
L=x(-20x+250)-4(-20x+250)
=-20x2+330x-1 000
=-20(x-
当且仅当x=8.25时,L取得最大值。
故当单价定为8.25元时,工厂可获得最大利润
知识点
已知向量 
正确答案
解析

知识点
已知




正确答案
(﹣5,0) ∪(5,﹢∞)
解析
做出





知识点
已知函数

(1)求
(2)设



正确答案
(1) -1
(2)
解析
(1)
(2)

∵
∴
∴
知识点
抛物线





正确答案
解析
知识点
不等式
正确答案
解析
知识点
若曲线


正确答案
解析
∵ 



知识点
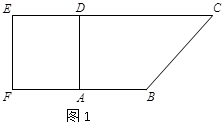
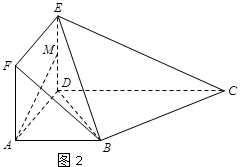
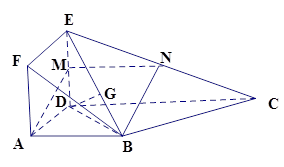
如图1,在直角梯形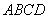
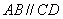
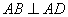
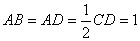
现以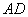
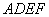
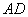
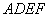
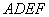
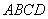
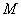
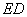
(1)求证: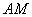
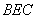
(2)求证: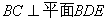
(3)求点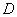
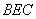
正确答案
见解析。
解析
(1)证明:
取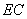
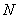
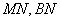
在△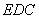
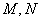
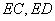
所以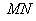
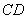
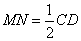
由已知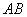
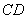
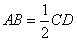
所以
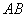
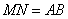
所以四边形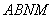
所以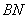
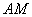
又因为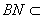
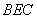
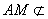
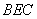
所以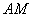
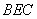
(2)在正方形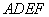
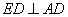
又因为平面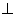
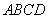
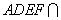
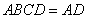
所以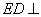

所以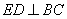
在直角梯形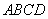
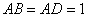

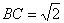
在△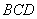
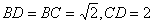
所以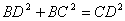
所以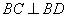
所以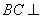

(3)解法一:因为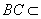
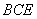
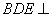
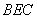
过点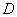
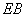
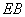
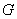
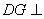
所以点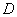
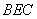
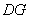
在直角三角形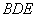
所以
所以点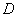
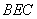
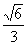
解法二: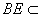
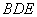
所以
又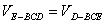
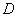
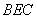
则 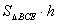
所以点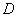
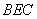
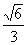
知识点
直线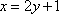
正确答案
解析
略
知识点




正确答案
解析
略
知识点
扫码查看完整答案与解析