- 直线和圆的方程
- 共1163题
如图,在平面直角坐标系


及其上一点
21.设圆





22.设平行于





23.设点





正确答案
解析
因为



则圆

又圆



则



考查方向
解题思路
易错点
圆的方程、直线方程的求法及表示,位置关系中的几何表示。
正确答案

解析
由题意得





则


解得




考查方向
解题思路
易错点
圆的方程、直线方程的求法及表示,位置关系中的几何表示。
正确答案

解析





即

对于任意

此时


必然与圆交于


因此对于任意
综上
考查方向
解题思路
易错点
圆的方程、直线方程的求法及表示,位置关系中的几何表示。
3.
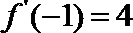

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.直线

正确答案
-7
解析
解析已在路上飞奔,马上就到!
知识点
11.输入x=2,运行下图的程序输出的结果为
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
8.已知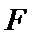



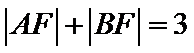


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若曲线
正确答案
(1,0)
解析
解析已在路上飞奔,马上就到!
知识点
当函数

正确答案
解析
由
由
当且仅当



知识点
已知抛物线的顶点为






(1)求抛物线的方程;
(2)圆






正确答案
见解析
解析
(1)设抛物线方程为


(2)设
由

则
由点


又
又

若存在





结合(*)得,
知识点
21.在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别是(﹣

(1)求△ABC的顶点C的轨迹E的方程;
(2)不过点A的直线l与轨迹E交于不同的两点P,Q.若以PQ为直径的圆过点A时,试判断直线l是否过定点?若过,请求出定点坐标,不过,说明理由.
正确答案
见解析。
解析
(1)设点C坐标为(x,y)
因为G为△ABC的重心故G点坐标为
由|MC|=|MB|得∴
即
∴△ABC的顶点C的轨迹E的方程是
(2)设直线
联立:
∴△=4k2b2﹣4(k2+3)(b2﹣6)=12(2k2﹣b2+6)>0,
且
若以PQ为直径的圆过点A时,则有
∴

故
代入整理得:

①当


且代入△>0成立; …(13分)
②当

综上知:直线过定点
知识点
20. 已知椭圆







(1)求椭圆
(2)已知点






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
不等式
正确答案

解析
略
知识点
为了了解1000名学生的学习情况,采用系统抽样的方法,从中抽取容量为40的样本,则分段的间隔为
正确答案
解析
略
知识点
扫码查看完整答案与解析