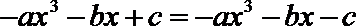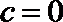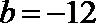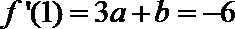- 直线和圆的方程
- 共1163题
17.设函数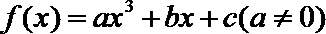
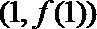
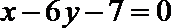
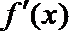
(1)求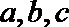
(2)求函数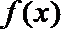
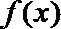
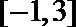
正确答案
(1)∵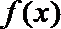
∴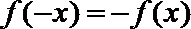
∴
∵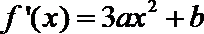
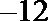
又直线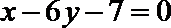

∴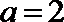
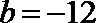
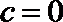
(2)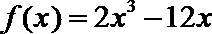
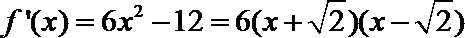
所以函数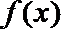
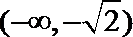
∵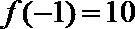
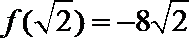
∴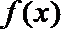
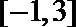
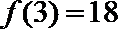
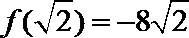
解析
解析已在路上飞奔,马上就到!
知识点
20. 设圆




(1)求圆
(2)过点






正确答案
(1)设圆F的方程为(x-1)2+y2=r2(r>0).
将y2=4x代入圆方程,得(x+1)2=r2,所以x=-1-r(舍去),或x=-1+r.
圆与抛物线有且只有一个公共点,当且仅当-1+r=0,即r=1.
故所求圆F的方程为(x-1)2+y2=1.
(2)设过点M(-1,0)与圆F相切的斜率为正的一条切线的切点为T.
连结TF,则TF⊥MT,且TF=1,MF=2,所以∠TMF=30°.
直线MT的方程为x=y-1,与y2=4x联立,得y2-4y+4=0.
记直线与抛物线的两个交点为A(x1,y1)、B(x2,y2),
则y1+y2=4,y1y2=4,x1+x2=(y1+y2)-2=10.
从而AB的垂直平分线的方程为y-2=-(x-5).
令y=0得,x=7.由圆与抛物线的对称性可知圆E的圆心为E(7,0).
|AB|=8.
又点E到直线AB的距离d=4,所以圆E的半径R=4.
因此圆E的方程为(x-7)2+y2=48.
解析
解析已在路上飞奔,马上就到!
知识点




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.


(1)求

(2)求切点坐标,求直线
正确答案
(1)k=-3
(2)设切点为
切线的斜率
代入到

解析
解析已在路上飞奔,马上就到!
知识点
6.已知A、B两点分别在两条互相垂直的直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知向量


(1)求函数
(2)若








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.曲线C:x|x|+y|y|=1
(I) 直线x+y-b=0与曲线C交于A,B两点用b表示|AB|的长;
(II) 分别过A,B作直线x+y=0的垂线,垂足分别为C,D,求四边形ABCD面积的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.若圆

正确答案
解析
画出草图,如图所示,据图可知F(1,0)为圆心,BF=2,BC=3,由此可以求得CF=

考查方向
解题思路
画出草图,
结合图形通过题目条件确定相应的几何关系关系,即可求出圆的半径即可。
易错点
本题容易因为对抛物线的标准方程记忆不清楚而导致题目做错。
知识点
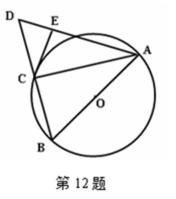
13.如图,AB是圆的直径,弦CD与AB相交于点E,BE=2AE=2,BD=ED,则线段CE的长为__________.
正确答案
知识点
5.圆(x+1)2+y2=2的圆心到直线y=x+3的距离为
正确答案
知识点
12.已知圆C的圆心在x轴的正半轴上,点


正确答案
知识点
12. 如图,
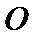
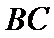
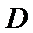
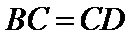
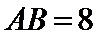
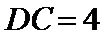
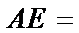
正确答案
3
解析
由题可知,a5=3a1+2a3,q4=3+2q2,q2=3,则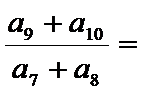
考查方向
解题思路
表示等差数列,表示首项与公比的关系,代入即可得到结果。
易错点
本题易在表示等差数列时发生错误。
知识点
11.函数

正确答案
0
解析
考查方向
本题主要考查了导数的几何意义/导数的几何意义是高频考点,主要涉及求切线方程、求参数。
解题思路
易错点
易求错函数的导函数。
知识点
扫码查看完整答案与解析