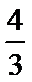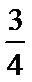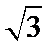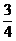直线和圆的方程_章节学习

1

题型：单选题

|

单选题 · 5 分

6. 圆x2+y2−2x−8y+13=0的圆心到直线ax+y−1=0的距离为1，则a=( )

A−

B−

C

D2

正确答案

A

知识点

点到直线的距离公式圆的标准方程

1

题型：单选题

|

单选题 · 5 分

圆x2+y2−2x−8y+13=0的圆心到直线ax+y−1=0的距离为1，则a=( )

A−

B−

C

D2

正确答案

A

知识点

点到直线的距离公式直线与圆的位置关系

1

题型：填空题

|

填空题 · 5 分

13.若直线与圆（）相交于A,B两点，且(O为坐标原点)，则 .

正确答案

2

解析

由得圆心（0,0）到直线的距离为，所以，所以。

考查方向

本题主要考察直线与圆的位置关系等问题，意在考察考生的数形结合能力。

解题思路

先求出圆心到直线的距离后利用点到直线的距离公式即可。

易错点

不知道题中给出的120度如何转换导致出错。

知识点

点到直线的距离公式直线与圆的位置关系直线和圆的方程的应用

1

题型：单选题

|

单选题 · 5 分

10.若椭圆的离心率，右焦点为，方程的两个实数根分别是，则点到直线的距离为（）

A1

B2

C3

D4

正确答案

A

解析

因为，得a=3c，所以，则方程为，所以，则点到直线的距离为

，所以选A.

考查方向

本题主要考查了圆锥曲线的问题。

解题思路

用设而不求的方法来做。

易错点

不会用设而不求的方法来做。

知识点

点到直线的距离公式椭圆的几何性质

1

题型：填空题

|

填空题 · 5 分

已知圆O：x2+y2=1和点A（﹣2，0），若定点B（b，0）（b≠﹣2）和常数λ满足：对圆O上任意一点M，都有|MB|=λ|MA|，则：

（1）b=　　；

（2）λ=　。

正确答案

（1）﹣；

（2）

解析

（1）设M（x，y），则

∵|MB|=λ|MA|，

∴（x﹣b）2+y2=λ2（x+2）2+λy2，

由题意，取（1，0）、（﹣1，0）分别代入可得（1﹣b）2=λ2（1+2）2，（﹣1﹣b）2=λ2（﹣1+2）2，

∴b=﹣，λ=。

（2）由（1）知λ=。

知识点

三点共线问题圆的标准方程

1

题型：简答题

|

简答题 · 13 分

已知，分别是椭圆的左、右焦点，关于直线的对称点是圆的一条直径的两个端点。

（1）求圆的方程；

（2）设过点的直线被椭圆和圆所截得的弦长分别为，。当最大时，求直线的方程。

正确答案

（1）

（2）

解析

（1）先求圆C关于直线x + y – 2 = 0对称的圆D，由题知圆D的直径为直线对称.

（2）由(Ⅰ)知(2,0), ,据题可设直线方程为: x = my +2,m∈R. 这时直线可被圆和椭圆截得2条弦，符合题意.

圆C:到直线的距离。

.

由椭圆的焦半径公式得：

.

所以当

知识点

圆的标准方程椭圆的几何性质直线与圆锥曲线的综合问题

1

题型：简答题

|

简答题 · 12 分

如图，已知椭圆：的离心率为，以椭圆的左顶点为圆心作圆：，设圆与椭圆交于点与点。

（1）求椭圆的方程；

（2）求的最小值，并求此时圆的方程；

（3）设点是椭圆上异于,的任意一点，且直线分别与轴交于点，为坐标原点，求证：为定值，

正确答案

见解析。

解析

（1）

故椭圆的方程为，

（2）点与点关于轴对称，设，，不妨设。

由于点在椭圆上，所以，（*）

由已知，则，，

。

由于，故当时，取得最小值为。

由（*）式，，故，又点在圆上，代入圆的方程得到，

故圆的方程为：，

（3）

知识点

向量在几何中的应用圆的标准方程椭圆的定义及标准方程直线与圆锥曲线的综合问题直线、圆及圆锥曲线的交汇问题

1

题型：单选题

|

单选题 · 5 分

已知圆的圆心是直线与轴的交点，且圆与直线相切，则圆的方程是

A

B

C

D

正确答案

A

解析

略

知识点

圆的标准方程

1

题型：填空题

|

填空题 · 5 分

若圆心在直线上、半径为的圆与直线相切，则圆的方程是_____.

正确答案

或

解析

略

知识点

圆的标准方程直线与圆的位置关系

1

题型：填空题

|

填空题 · 5 分

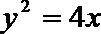
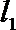
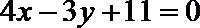
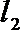
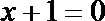
15．已知P是抛物线上的一个动点，则P到直线：和：的距离之和的最小值是（）

正确答案

3

解析

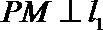
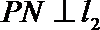
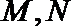
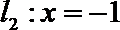
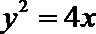
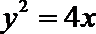
过点P作，，垂足分别为，是抛物线的准线方程，抛物线的焦点为F(1，0)；

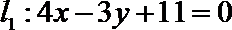
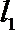
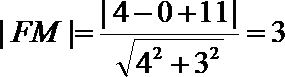
由抛物线的定义，得|PN|=|PF|，过点P作直线的垂线，垂足为M，所以|PM|+|PN|=|PM|+|PF|,当三点M，P，F共线时，|PM|+|PF|取得最小值，其最小值为点F到直线的距离，所以；

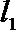
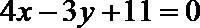
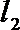
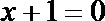
所以P到直线：和：的距离之和的最小值是3。

考查方向

本题主要考查了抛物线的定义和标准方程。

易错点

本题易在得到|PN|=|PF|时出现错误，易忽视“利用抛物线的定义将抛物线上的点到准线的距离转化为到焦点的距离”的应用．

知识点

点到直线的距离公式抛物线的标准方程和几何性质

1

题型：填空题

|

填空题 · 4 分

若圆的半径为1，圆心在第一象限，且与直线和轴都相切，则该圆的标准方程是_____.

正确答案

解析

略

知识点

圆的标准方程

1

题型：简答题

|

简答题 · 15 分

已知可行域的外接圆C与x轴交于点A1、A2，椭圆C1以线段A1A2为长轴，离心率。

（1）求圆C及椭圆C1的方程；

（2）设椭圆C1的右焦点为F，点P为圆C上异于A1、A2的动点，过原点O作直线PF的垂线交直线于点Q，判断直线PQ与圆C的位置关系，并给出证明。

正确答案

见解析

解析

(1)由题意可知，可行域是以及点为顶点的三角形，

∵，∴为直角三角形，

∴外接圆C以原点O为圆心，线段A1A2为直径，故其方程为。

∵2a=4，∴a=2，又，∴，可得。

∴所求椭圆C1的方程是。

（2）直线PQ与圆C相切，设，则。

当时，，∴；

当时，

∴直线OQ的方程为，因此，点Q的坐标为。

∵，

∴当时，，；

当时候，，∴。

综上，当时候，，故直线PQ始终与圆C相切。

知识点

二元一次不等式（组）表示的平面区域圆的标准方程直线与圆的位置关系椭圆的定义及标准方程直线与圆锥曲线的综合问题

1

题型：单选题

|

单选题 · 5 分

圆关于直线对称的圆的方程为

A

B

C

D

正确答案

A

解析

略

知识点

圆的标准方程

1

题型：填空题

|

填空题 · 5 分

以抛物y2＝4x的焦点为圆心且与双曲线的渐近线相切的圆的方程

是＿＿＿＿

正确答案

解析

略

知识点

圆的标准方程椭圆的几何性质抛物线的标准方程和几何性质直线、圆及圆锥曲线的交汇问题

1

题型：单选题

|

单选题 · 5 分

若圆C经过(1，0)，(3，0)两点，且与y轴相切，则圆C的方程为

A

B

C

D

正确答案

D

解析

略

知识点

圆的标准方程

热门试卷

正确答案

知识点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

易错点

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点