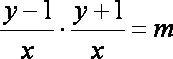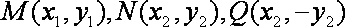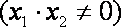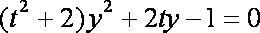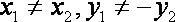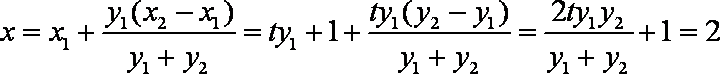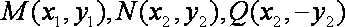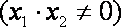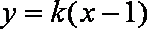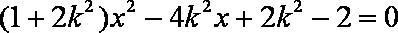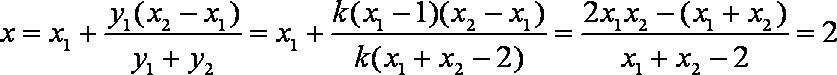- 直线和圆的方程
- 共1163题
已知


(1)求
(2)已知点





(3)若点






正确答案
见解析
解析
(1)由


(2)由


由





此时

(3)设点




又



故


知识点
已知圆O的内接△ABC中,D为BC上一点,且△ADC为正三角形,点E为BC的延长线上一
点,AE为圆O的切线,求证:CD2=BD·EC。
正确答案
见解析。
解析
因为AE为圆O的切线,所以∠ABD=∠CAE,
因为△ACD为等边三角形,所以∠ADC=∠ACD,
所以∠ADB=∠ECA,所以△ABD∽△EAC,
所以
因为△ACD为等边三角形,所以AD=AC=CD,
所以CD2=BD·EC.
知识点
在平面直角坐标系xOy中,直线l的参数方程为

正确答案
解析
直线方程为y=x+1,圆的方程为(x﹣1)2+y2=1。
于是圆心(1,0)到直线x﹣y+1=0的距离为
故答案为:
知识点
已知圆C方程:(x-1)2 + y 2=9,垂直于x轴的直线L与圆C相切于N点(N在圆心C的右侧),平面上有一动点P,若PQ⊥L,垂足为Q,且
(1)求点P的轨迹方程;
(2)已知D为点P的轨迹曲线上第一象限弧上一点,O为原点,A、B分别为点P的轨迹曲线与x,y轴的正半轴的交点,求四边形OADB的最大面积及D点坐标.
正确答案
见解析。
解析
(1)设

则
因为

化简得
所以点
(2)依题意得,


设

则四边形

又因为
所以
所以四边形

当四边形


此时
知识点
已知椭圆




(1)求椭圆
(2)设点



(3)过点








正确答案
见解析
解析
(1)由已知可得 
所求椭圆方程为
(2)设点


则
由


得
(3)若直线



设

由 

则
由已知
所以
即
所以

故直线




所以直线

若直线


设

由已知
得



综上,直线

知识点
已知△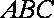
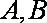
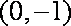
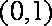
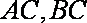
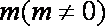
(1)求顶点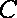
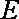
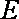
(2)当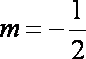
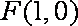
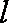
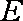
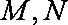
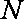
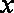
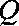
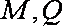
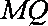
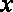
正确答案
见解析
解析
(1)由题知:
化简得: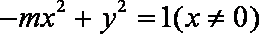
当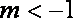
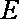
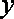
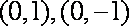
当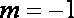
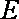
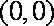
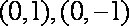
当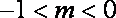
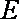
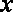
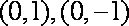
当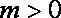
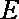
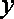
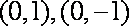
……………………6分
(2)设
依题直线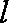
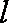
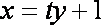
代入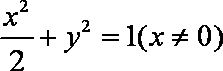
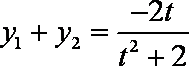
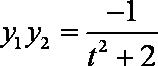
又因为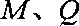
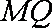
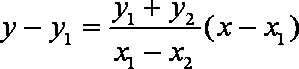
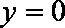
得
故直线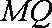
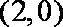
解二:设
依题直线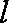
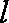
代入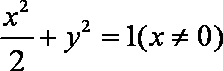
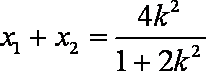
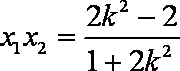
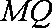
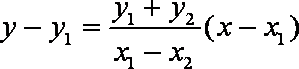
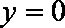
得
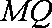
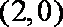
知识点
如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直直线AB。点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点。
(1)若∠PAB=30°,求以MN为直径的圆方程;
(2)当点P变化时,求证:以MN为直径的圆必过圆O内的一定点。
正确答案
见解析。
解析
建立如图所示的直角坐标系,
⊙O的方程为
直线L的方程为
(1)∵∠PAB=30°,∴点P的坐标为
∴

将x=4代入,得
∴MN的中点坐标为(4,0),MN=
∴以MN为直径的圆的方程为
同理,当点P在x轴下方时,所求圆的方程仍是
(2)设点P的坐标为



∵
将x=4代入,得



MN的中点坐标为
以MN为直径的圆

∴⊙

知识点
已知过某定圆上的每一点均可以作两条相互垂直的直线与椭圆
正确答案
解析
易得椭圆

的外接圆,方程为

垂直的直线与椭圆
知识点
已知F1、F2分别是椭圆

正确答案

解析
∵椭圆

设k=

则当|PF1|=|PF2|时,k取得最小值0;
当|PF2|=a+c=



∴k的取值范围是
故答案为
知识点
在圆

正确答案

解析
圆的半径是2,圆心






知识点
如图,F1,F2是双曲线C:
正确答案
解析
∵|AB|:|BF2|:|AF2|=3:4:5,不妨令|AB|=3,|BF2|=4,|AF2|=5,
∵|AB|2+

∴∠ABF2=90°,
又由双曲线的定义得:|BF1|﹣|BF2|=2a,|AF2|﹣|AF1|=2a,
∴|AF1|+3﹣4=5﹣|AF1|,
∴|AF1|=3。
∴|BF1|﹣|BF2|=3+3﹣4=2a,
∴a=1。
在Rt△BF1F2中,



∴4c2=52,
∴c=
∴双曲线的离心率e=

知识点
如图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2。
(1)求AC的长;
(2)试比较BE与EF的长度关系。
正确答案
(1)
解析
(1)

又




(2)




知识点
设地球半径为R,若甲地位于北纬45°东经120°,乙地位于南纬度75°东经120°,则甲、乙两地球面距离为( )
正确答案
解析
解:由于甲、乙两地都在东经120°,就是都在同一个大圆上,
它们的纬度差是:120°,就是大圆周的
则甲、乙两地球面距离为:
知识点
在极坐标系中,圆C的方程为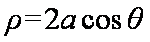
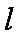
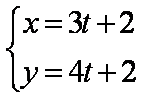
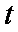
(1)若直线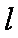
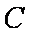
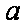
(2)若直线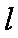
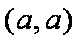
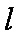
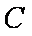
正确答案
见解析。
解析
(1)易求得直线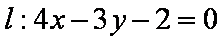

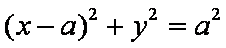
依题意,有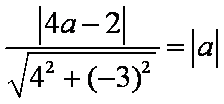
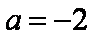
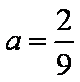
(2)因为直线
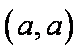
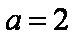

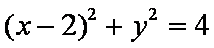
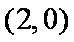
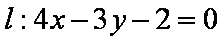
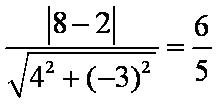
故弦长为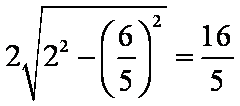
知识点
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立坐标系,直线




(1)求点Q的轨迹
(2)直线


正确答案
见解析
解析
(1)由题意知,曲线
设P(




(2)直线l的普通方程y=ax,由题意得:

知识点
扫码查看完整答案与解析