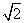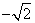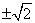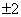- 直线和圆的方程
- 共1163题
在极坐标系中,直线





正确答案
-1或-5
解析
略
知识点
若直线
正确答案
解析
略
知识点
设圆C位于抛物线y2=2x与直线x=3所围成的封闭区域(包含边界)内,则圆C的半径能取到的最大值为________。
正确答案
解析
由题意知,半径取得最大值的圆的圆心必在x轴上。
设圆心C(a,0)(0<a<3),则半径为3-a,于是圆的方程为(x-a)2+y2=(3-a)2,
将抛物线方程y2=2x代入圆的方程得
(x-a)2+2x=(a-3)2,即x2-2(a-1)x+6a-9=0,
由Δ=4(a-1)2-4(6a-9)=0,即a2-8a+10=0,解得
知识点
已知






正确答案
解析
略
知识点
已知直线l: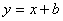
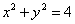
正确答案
解析
略
知识点
已知可行域

(1)求圆C及椭圆C1的方程;
(2)设椭圆C1的右焦点为F,点P为圆C上异于A1、A2的动点,过原点O作直线PF的垂线交直线
正确答案
见解析
解析
(1)由题意可知,可行域是以

∵

∴外接圆C以原点O为圆心,线段A1A2为直径,故其方程为
∵2a=4,∴a=2,又


∴所求椭圆C1的方程是
(2)直线PQ与圆C相切,设

当


当
∴直线OQ的方程为

∵
∴当


当


综上,当

知识点
已知直线
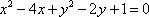
正确答案
-12或8
解析
略
知识点
如图3,已知








正确答案
解析
略
知识点
如图,













正确答案
2
解析
如下图:
知识点
圆



正确答案

解析
略
知识点
若直线


正确答案
解析
略
知识点
圆

正确答案
1
解析
略
知识点
已知直线




正确答案
-6
解析
略
知识点
直线

正确答案
解析
略
知识点
已知圆C:

正确答案
解析
圆的半径为








知识点
扫码查看完整答案与解析