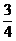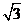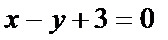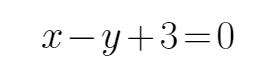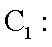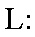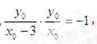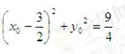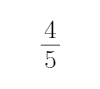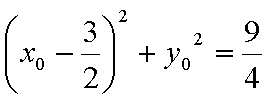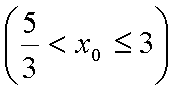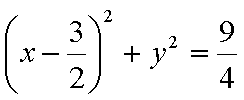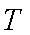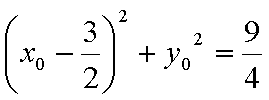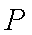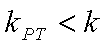直线和圆的方程_章节学习

1

题型：填空题

|

填空题 · 5 分

15.已知直线l：与圆x2+y2=12交于A、B两点，过A、B分别作l的垂线与x轴交于C、D两点，则|CD|=______.

正确答案

4

知识点

直线与圆的位置关系相交弦所在直线的方程

1

题型：单选题

|

单选题 · 5 分

圆x2+y2−2x−8y+13=0的圆心到直线ax+y−1=0的距离为1，则a=( )

A−

B−

C

D2

正确答案

A

知识点

点到直线的距离公式直线与圆的位置关系

1

题型：填空题

|

填空题 · 5 分

13.若直线与圆（）相交于A,B两点，且(O为坐标原点)，则 .

正确答案

2

解析

由得圆心（0,0）到直线的距离为，所以，所以。

考查方向

本题主要考察直线与圆的位置关系等问题，意在考察考生的数形结合能力。

解题思路

先求出圆心到直线的距离后利用点到直线的距离公式即可。

易错点

不知道题中给出的120度如何转换导致出错。

知识点

点到直线的距离公式直线与圆的位置关系直线和圆的方程的应用

1

题型：填空题

|

填空题 · 5 分

14.已知M,N是圆与圆的公共点，则的面积为________.

正确答案

解析

∵圆,则；

圆，则

∴MN的方程为

∴,

∴

考查方向

本题主要考查了圆与圆的位置关系

解题思路

先求出两圆的公共弦MN的方程，然后利用点B到直线MN的距离求出高BE，利用勾股定理求出MN即可

易错点

本题必须注意利用两圆相间得到公共弦方程

知识点

直线与圆的位置关系

1

题型：单选题

|

单选题 · 5 分

3.在区间上随机取一个数，使直线与圆相交的概率为

A

B

C

D

正确答案

C

解析

因为直线与圆相交，所以圆心到直线的距离小于半径，圆心为，半径为1，直线方程化为一般式得，由点到直线的距离公式可得，解得，所以概率为，所以应选C选项。

考查方向

本题主要考查几何概型，以及直线和圆的位置关系，几何概型高考经常以小题的形式出现，常与其他知识点结合一起考，难度较大.

解题思路

1)用圆心到直线的距离小于半径，得到的取值范围；

2)用的范围与作商，求出概率；

易错点

本题易将几何概型当成古典概型去做，只取整数点比较.

知识点

直线与圆的位置关系直线和圆的方程的应用与长度、角度有关的几何概型

1

题型：填空题

|

填空题 · 5 分

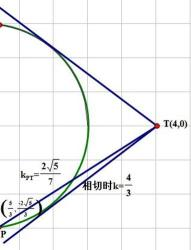
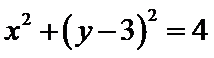
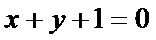
13．已知直线过圆的圆心，且与直线垂直，则直线的方程为 .

正确答案

解析

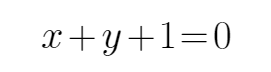
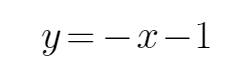
由题意可知，直线化为所求直线与它垂直，所以直线的斜率为k=1,又圆心为（0，3），由点斜式可得：

考查方向

直线与圆的关系，直线的方程

解题思路

根据直线和直线垂直，然后求直线斜率，进而求直线的方程

易错点

知识点

直线与圆的位置关系

1

题型：填空题

|

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1

题型：填空题

|

填空题 · 5 分

已知直线与圆心为的圆相交于两点，且

，则实数的值为_________.

正确答案

0或6

解析

将圆配方得，故圆心，半径，由已知为等腰直角三角形，故,圆心到直线的距离，所以：

或

知识点

圆与圆的位置关系及其判定

1

题型：单选题

|

单选题 · 5 分

8．从圆外一点向这个圆作两条切线，则两切线夹角的余弦值为（）

A

B

C

D0

正确答案

B

解析

圆x2-2x+y2-2y+1=0的圆心为M（1，1），半径为1，从外一点P（3，2）向这个圆作两条切线，则点P到圆心M的距离等于，每条切线与PM的夹角的正切值等于，所以两切线夹角的正切值为，，该角的余弦值等于

考查方向

本题主要考查了圆的切线方程；

解题思路

先求出点P到圆心M的距离等于，每条切线与PM的夹角的正切值等于，然后利用夹角公式求出即可

易错点

本题易在圆外一点求圆的切线方程，注意数形结合；

知识点

两直线的夹角与到角问题直线与圆的位置关系

1

题型：简答题

|

简答题 · 14 分

20．已知过原点的动直线与圆相交于不同的两点，。

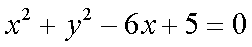
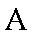
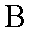
（1）求圆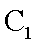的圆心坐标；

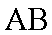
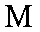
（2）求线段的中点的轨迹的方程；

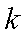
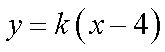
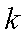
（3）是否存在实数，使得直线与曲线只有一个交点？若存在，求出的取值范围；若不存在，说明理由。

正确答案

（1）圆C1：X2+Y2-6X+5=0化为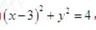,所以圆C1的圆心坐标为（3,0）

（2）设线段AB的终点M（x0，y0），由圆的性质可得C1M垂直于直线L

设直线L的方程为y=mx，所以,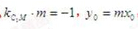

所以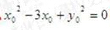即

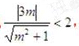
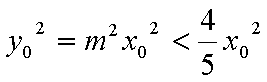
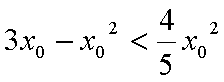
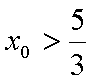
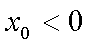
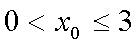
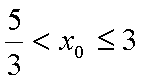
因为动直线L与圆C1相交，所以所以m2<

所以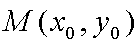，所以，解得或，又因为，所以。

所以满足

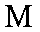
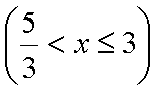
即的轨迹的方程为。

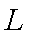
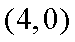
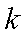
（3）由题意知直线表示过定点，斜率为的直线。

结合图形，表示的是一段关于X轴对称，起点为按逆时针方向运动到的圆弧.根据对称性，只需讨论在X轴对称下方的圆弧.设，则,而当直线与轨迹相切时，，解得.在这里暂取，因为，所以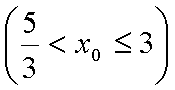

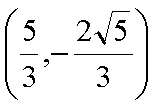
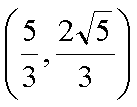
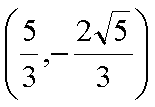
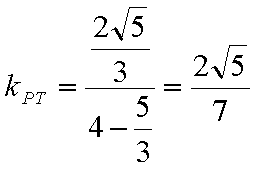
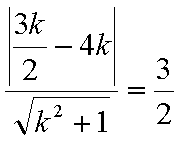
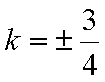
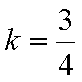
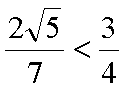
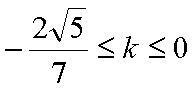
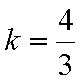
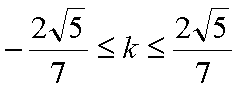
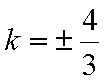
结合图形，可得对于X轴对称下方的圆弧，当或时，直线L与X轴对称下方的圆弧有且只有一个交点，根据对称性可知或。

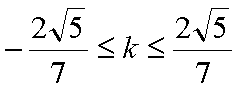
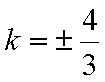
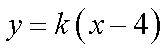
综上所述：当或时，直线L：与曲线只有一交点。

解析

解析已在路上飞奔，马上就到！

知识点

直线与圆的位置关系直线与圆相交的性质与圆有关的轨迹问题

1

题型：填空题

|

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1

题型：单选题

|

单选题 · 5 分

执行如图所示的程序框图，输出的值为（）

A

B

C

D

正确答案

C

解析

当k=0时，；当k=1时，；

当k=2时，；当k=3时，输出，故选C.

知识点

圆与圆的位置关系及其判定

1

题型：简答题

|

简答题 · 10 分

在直角坐标系xOy中，设倾斜角为α的直线l：(t为参数)与曲线C：(θ为参数)相交于不同两点A，B。

(1)若，求线段AB中点M的坐标；

(2)若|PA|·|PB|＝|OP|2，其中P(2，)，求直线l的斜率。

正确答案

（1）(，)（2）

解析

设直线l上的点A，B对应参数分别为t1，t2，将曲线C的参数方程化为普通方程＋y2＝1。

(1)当时，设点M对应参数为t0。

直线l方程为(t为参数)，

代入曲线C的普通方程＋y2＝1，得13t2＋56t＋48＝0，

则，所以，点M的坐标为(，)。

(2)将代入曲线C的普通方程＋y2＝1，得

(cos2α＋4sin2α)t2＋(sinα＋4cosα)t＋12＝0，

因为|PA|·|PB|＝|t1t2|＝，|OP|2＝7，

所以，得。

由于＝32cosα(sinα－cosα)＞0，

故。

所以直线l的斜率为

知识点

圆与圆的位置关系及其判定

1

题型：单选题

|

单选题 · 5 分

圆与圆的位置关系为

A内切

B相交

C外切

D相离

正确答案

B

解析

两圆的圆心分别为，，半径分别为，两圆的圆心距离为，则，所以两圆相交，选B.

知识点

圆与圆的位置关系及其判定

1

题型：填空题

|

填空题 · 5 分

已知是递增的等比数列，若，，则此数列的公比。

正确答案

2

解析

或

∵是递增的等比数列，∴

知识点

圆与圆的位置关系及其判定

热门试卷

正确答案

知识点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点