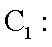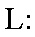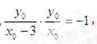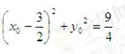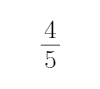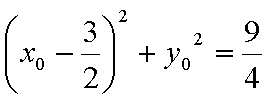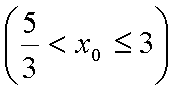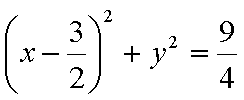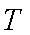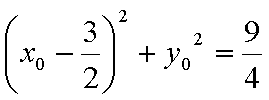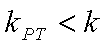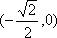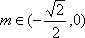- 直线和圆的方程
- 共1163题
12.过点






正确答案
解析
有割线定理得,(PC-


设A(x,y),则(x+4)2+y2=10与圆
x=-1, y=


考查方向
解题思路
直线与圆相交的问题,常常考查求弦长问题,涉及到弦的中点即可使用圆的相关的几何性质,转化为直线垂直,进而求出斜率,使用点斜式求出方程。
易错点
1、本题点

2、两直线垂直的等价条件不能与直线的斜率联系起来。
知识点
14. 已知过点



正确答案
【答案】x-3y-6=0 ,
解析
由已知可得圆的半径为5,而弦长刚好等于直径,所以直线经过圆心,由直线方程的两点式方程可以求出直线的方程为x-3y-6=0。
考查方向
解题思路
本题可以将已知条件转化到弦长和半径以及圆心到直线的距离所构成的直角三角形中去利用勾股定理算出圆心到直线的距离,然后利用点到直线的距离构造一个关于斜率的方程解出即可。
易错点
本题不知道将已知转化到弦长和半径以及圆心到直线的距离所构成的直角三角形中去求解。
知识点
13. 已知圆

若




正确答案
解析
由题可知,圆心到l1的距离为d=√2,则圆心到l2的距离为√3,代入点到直线的距离公式,可求得k=
考查方向
解题思路
利用垂径定理求解即可
易错点
本题易在表示弦长时发生错误。
知识点
12.已知圆C的圆心坐标为

正确答案
解析
.
根据抛物线几何性质可知准线方程

所以圆的标准方程为
考查方向
解题思路
该题思路比较清晰,主要有以下几个步骤1、写出准线方程


易错点
本题易错点主要集中在准线的表达,弦长公式的表达
知识点
13. 已知圆


正确答案
2或6
解析
由勾股定理知,圆心到直线的距离等于
由点到直线的距离知,圆心到直线的距离等于


考查方向
本题考查了圆与直线的相交弦问题.
解题思路
利用不同的计算方法,得到等量关系.
易错点
本题如使用弦长公式求解,会使得问题复杂化.
知识点
10.已知直线


正确答案
解析
由题意,得





考查方向
本题主要考查了直线与圆的位置关系,在近几年的各省高考题中出现的频率较高,常与三角形、点到直线的距离等知识交汇命题。
易错点
本题易在由



知识点
13.已知过点

正确答案

解析
考查方向
解题思路
1、设直线方程(注意斜率不存在的情况)
2、使用弦长公式求出圆心到直线的距离
3、使用点到直线的距离公式计算圆心到直线的距离求出k并得出最终结果
易错点
本题易于在设直线方程忽略斜率不存在的情况,导致漏解
知识点
14.已知圆O:
正确答案
解析
设AC中点P(x,y)OP⊥AP,
AC=2PM,PM∈[

考查方向
解题思路
本题考查运用曲线的方程与几何图形知识解决问题的能力,先设AC中点P(x,y)OP⊥AP,AP=
AC=2PM,PM∈[

易错点
本题必须运用几何性质找曲线的方程,否则无从下手。
知识点
20. 已知过点

(1)求k的取值范围;
(2)若

正确答案
(1)由题设,可知直线

因为

解得 
所以k的取值范围为
(2)设
将


所以

由题设可得

故圆心C在

解析
解析已在路上飞奔,马上就到!
知识点
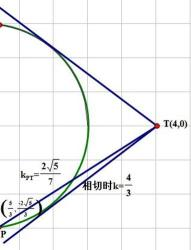
20.已知过原点的动直线
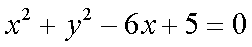
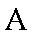
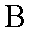
(1)求圆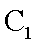
(2)求线段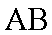
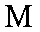

(3)是否存在实数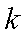
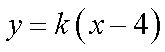

正确答案
(1)圆C1:X2+Y2-6X+5=0化为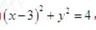
(2)设线段AB的终点M(x0,y0),由圆的性质可得C1M垂直于直线L
设直线L的方程为y=mx,所以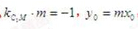
所以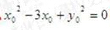
因为动直线L与圆C1相交,所以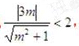
所以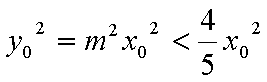
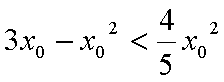
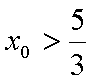
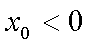
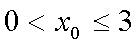
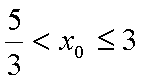
所以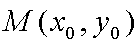
即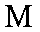

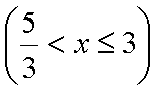
(3)由题意知直线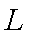
结合图形,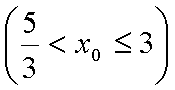
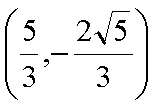
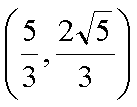
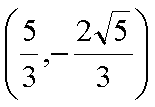
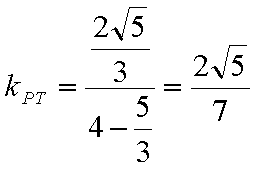

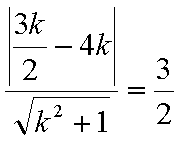
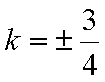
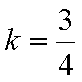
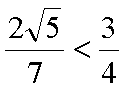
结合图形,可得对于X轴对称下方的圆弧,当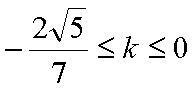
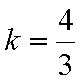
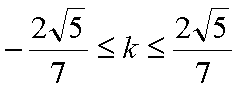
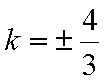
综上所述:当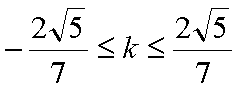
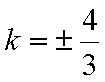
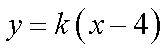

解析
解析已在路上飞奔,马上就到!
知识点
15.设直线y=x+2a与圆C:x2+y2-2ay-2=0相交于A,B两点,若|AB|=
则圆C的面积为 .
正确答案
1
知识点
已知函数
(1) 求
(2) 若对于任意的



正确答案
见解析
解析
知识点
抛物线y=
正确答案
解析
抛物线y=
∴
∴准线方程 y=﹣
知识点
设命题p:

正确答案
解析
因为全称命题的否定为特称命题,所以


知识点
已知函数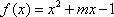
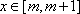
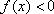
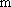
正确答案
解析
二次函数开口向上,在区间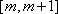
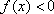
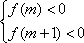
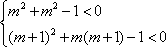
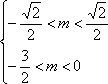
知识点
扫码查看完整答案与解析