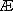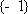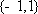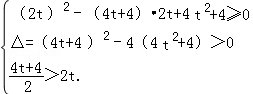集合与常用逻辑用语
共1759题

集合与常用逻辑用语
共1759题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

对于集合M，定义函数对于两个集合M，N，定义集合. 已知A={2，4，6，8，10}，B={1，2，4，8，16}。

（1）写出和的值，并用列举法写出集合；

（2）用Card(M)表示有限集合M所含元素的个数。

（ⅰ）求证：当取得最小值时，；

（ⅱ）求的最小值。

正确答案

见解析

解析

（1）解：，，.…………………3分

（2）设当取到最小值时，.

（ⅰ）证明：假设，令.

那么

.这与题设矛盾。

所以，即当取到最小值时，. …………7分

（ⅱ）同（ⅰ）可得：且.

若存在且，则令.

那么

所以集合中的元素只能来自.

若且，同上分析可知：集合中是否包含元素，的值不变。

综上可知，当为集合{1,6,10,16}的子集与集合{2,4,8}的并集时，取到最小值4. ………………………………………14分

知识点

集合的含义

题型：单选题

单选题 · 5 分

已知全集为

B{4}

C{0，2，4}

D{1，3}

正确答案

解析

略

知识点

集合的含义

题型：单选题

单选题 · 5 分

已知集合,则

正确答案

解析

略

知识点

集合的含义

题型：简答题

简答题 · 14 分

如图，在四棱柱中，已知底面是边长为的正方形，侧棱垂直于底面，且。

（1）点在侧棱上，若，

求证：平面；

（2）求三棱锥的体积。

正确答案

见解析。

解析

（1）依题意，，，在中，

同理可知，，（每式1分）

所以，

则，

同理可证，，

由于，平面，平面，

所以，平面，

解法2、

由（或）和证明平面（证明任何一个线线垂直关系给5分，第二个线线垂直关系给1分）

（2）解法1、

知识点

集合的含义

题型：单选题

单选题 · 5 分

设集合A＝{x|x2－2x－3＜0，x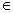R}，集合B＝{－2,2}，则A∩B为

A（－1,2）

B（－2,－1）

C（－2,3）

D（－2,2）

正确答案

解析

略

知识点

集合的含义

题型：单选题

单选题 · 5 分

设集合，集合，则等于

正确答案

解析

略

知识点

集合的含义

题型：填空题

填空题 · 5 分

将集合{|且}中的元素按上小下大，

左小右大的原则排成如图的三角形数表，将数表中位于

第行第列的数记为（）,则= .

正确答案

解析

略

知识点

集合的含义

题型：单选题

单选题 · 5 分

已知集合，，那么=（）

正确答案

解析

略

知识点

集合的含义

题型：单选题

单选题 · 5 分

已知集合，，则（∁）＝

A{1，2，3，4}

B{2，3，4}

C{3，4}

D{4}

正确答案

解析

略

知识点

集合的含义

题型：单选题

单选题 · 5 分

设集合A＝{x|x2－2x－3＜0，xR}，集合B＝{－2,2}，则A∩B为

A（－1,2）

B（－2,－1）

C（－2,3）

D（－2,2）

正确答案

解析

略

知识点

集合的含义

题型：单选题

单选题 · 5 分

集合，则=

正确答案

解析

略

知识点

集合的含义

题型：单选题

单选题 · 5 分

设集合A={x|x2﹣2x﹣3＜0，x∈R}，集合B=（﹣2，2），则A∩B为（　　）

A（﹣1，2）

B（﹣2，﹣1）

C（﹣2，3）

D（﹣2，2）

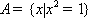
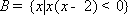
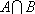
正确答案

解析

：A={x|x2﹣2x﹣3＜0，x∈R}=（﹣1，3）

∵B={﹣2，2}，

∴A∩B=（﹣1，2）

故选：A。

知识点

集合的含义

题型：填空题

填空题 · 5 分

已知集合，集合.若为坐标原点，，为集合所表示的平面区域与集合所表示的平面区域的边界的交点,则的面积与的关系式为（）。

正确答案

解析

略

知识点

集合的含义

题型：单选题

单选题 · 5 分

已知集合A={3，a2}，集合B={0，b，1﹣a}，且A∩B={1}，则A∪B=（　　）

A{0，1，3}

B{1，2，4}

C{0，1，2，3}

D{0，1，2，3，4}

正确答案

解析

∵A={3，a2}，集合B={0，b，1﹣a}，且A∩B={1}，

∴a2=1，解得：a=1或a=﹣1，

当a=1时，1﹣a=1﹣1=0，不合题意，舍去；

当a=﹣1时，1﹣a=1﹣（﹣1）=2，此时b=1，

∴A={3，1}，集合B={0，1，2}，

则A∪B={0，1，2，3}。

故选C

知识点

集合的含义

题型：简答题

简答题 · 14 分

已知集合M是同时满足下列两个性质的函数f（x）的全体：

①f（x）在其定义域上是单调增函数或单调减函数；

②在f（x）的定义域内存在区间[a，b]，使得f（x）在[a，b]上的值域是。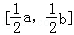

（1）判断函数y=﹣x3是否属于集合M？并说明理由，若是，请找出区间[a，b]；

（2）若函数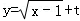∈M，求实数t的取值范围。

正确答案

见解析。

解析

（1）y=﹣x3的定义域是R，

∵y/=﹣3x2≤0，∴y=﹣x3在R上是单调减函数。

则y=﹣x3在[a，b]上的值域是[﹣b3，﹣a3]。

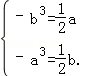
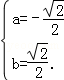
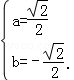
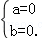
由解得：或（舍去）或（舍去）

∴函数y=﹣x3属于集合M，且这个区间是。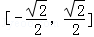

（2）设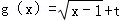，则易知g（x）是定义域[1，+∞）上的增函数。

∵g（x）∈M，∴存在区间[a，b]⊂[1，+∞），满足，。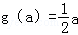

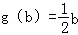
即方程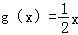在[1，+∞）内有两个不等实根。

[法一]：方程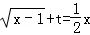在[1，+∞）内有两个不等实根，

等价于方程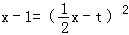在[2t，+∞）内有两个不等实根。

即方程x2﹣（4t+4）x+4t2+4=0在[2t，+∞）内有两个不等实根。

根据一元二次方程根的分布有

解得。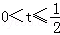

因此，实数t的取值范围是。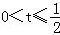

[法二]：要使方程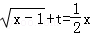在[1，+∞）内有两个不等实根，

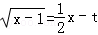
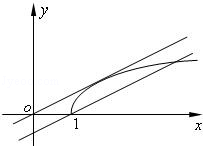
即使方程在[1，+∞）内有两个不等实根。

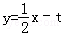
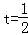
如图，当直线经过点（1，0）时，，

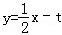
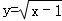
当直线与曲线相切时，

方程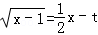两边平方，得x2﹣（4t+4）x+4t2+4=0，由△=0，得t=0。

因此，利用数形结合得实数t的取值范围是。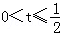

知识点

集合的含义

继续学习学习下一知识点

下一知识点 : 函数的概念与基本初等函数

百度题库 > 高考 > 文科数学 > 集合与常用逻辑用语

扫码查看完整答案与解析