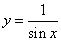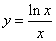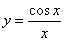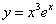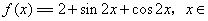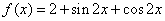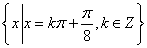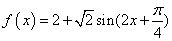- 函数的概念与基本初等函数
- 共5812题
已知函数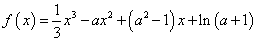
(1)若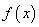
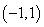
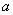
(2)若存在一条与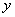
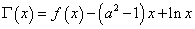

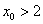
(3)记函数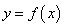
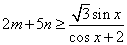
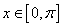
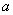
正确答案
见解析。
解析
知识点
若函数
那么方程
正确答案
解析
略
知识点
下列函数中,与函数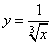
正确答案
解析
略
知识点
设函数
正确答案
解析
略
知识点
已知命题








正确答案
解析
略
知识点
已知变量x,y满足约束条件
正确答案
解析
由约束条件作出可行域如图所示,
当z=x+2y过点A时z取得最小值,联立方程组
∴zmin=-1+2×(-2)=-5.
知识点
方程组
正确答案
解析
略
知识点
已知函数
(1)函数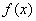
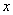
(2)函数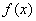
正确答案
见解析。
解析
(1)

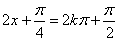

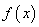
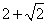
因此,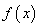
(2)
由题意得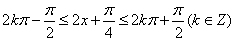
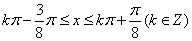
因此,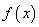
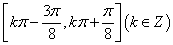
知识点
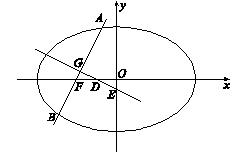
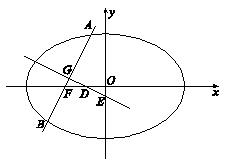
如图,已知椭圆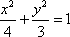
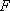

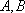
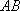
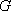
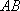

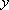
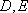
(1)若点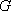
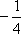
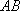
(2)记△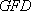
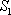
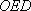

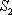
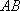
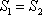
正确答案
见解析
解析
(1)解:依题意,直线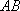
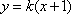
将其代入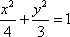
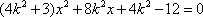
设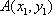
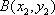
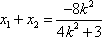
故点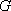
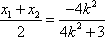
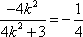
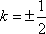
(2)解:假设存在直线
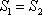
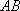
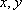
由(1)可得 
因为 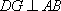
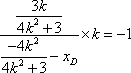
解得 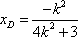
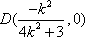
因为 △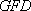

所以 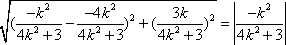
整理得 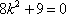

知识点
已知集合

正确答案
解析
略
知识点
函数
正确答案
解析
略
知识点
函数f(x)=sinxcosx的最小正周期是_________。
正确答案
π
解析
∵ sin2x=2sinxcosx
∴ f(x)=sinxcosx=
因此,函数f(x)的最小正周期T=
知识点
在△ABC中,角A,B,C的对边分别为a,b,c,cosA=

(1)求a的值;
(2)求sinC及△ABC的面积。
正确答案
(1)a=
(2)
解析
(1)因为

由正弦定理:


(2)在△ABC中,sinC=sin(A+B)=
△ABC的面积为:
知识点
已知函数




正确答案
解析
略
知识点
定义:



(1)若
(2)当

(3)求证:
正确答案
见解析。
解析
知识点
扫码查看完整答案与解析