- 带电粒子在混合场中的运动
- 共247题
11.如图所示的平面直角坐标系中,虚线OM与x轴成45°角,在OM与x轴之间(包括x轴)存在垂直纸面向里、磁感应强度大小为B的匀强磁场,在y轴与OM之间存在竖直向下、电场强度大小为E的匀强电场,有一个质量为m,电荷量为q的带正电的粒子以某速度沿x轴正方向从O点射入磁场区域并发生偏转,不计带电粒子的重力和空气阻力,在带电粒子进入磁场到第二次离开电场的过程中,求:
(1)若带电粒子从O点以速度v1进入磁场区域,求带电粒子第一次离开磁场的位置到O点的距离。
(2)若带电粒子第二次离开电场时恰好经过O点,求粒子最初进入磁场时速度v的大小,并讨论当v变化时,粒子第二次离开电场时的速度大小与v大小的关系。
正确答案
(1)粒子在磁场中做匀速圆周运动,根据牛顿第二定律有

解得
设粒子从N点离开磁场,如图所示,由几何知识可知
ON=
联立②③两式解得:
(2)粒子第二次离开磁场后在电场中做类平抛运动,若粒子第二次刚好从O点离开电场,则:
水平位移
解得:
竖直位移
而
联立⑥⑦⑧式并解得
①若


则粒子离开电场时的速度
②若
x=vt ⑬

则粒子离开电场时的速度
解析
解析已在路上飞奔,马上就到!
知识点
15.如图所示,在场强为E方向水平向左的匀强电场和磁感应强度为B垂直纸面向里的匀强磁场区域内,固定着一根足够长的粗糙的绝缘杆,杆上套着一个质量为m,带有电荷量-q的小球(q>0)。小球由静止开始沿杆下滑,则下列说法正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.如图所示,a、b是一对水平放置的平行金属板,板间存在着竖直向下的匀强电场。一个不计重力的带电粒子从两板左侧正中位置以初速度v沿平行于金属板的方向进入场区,带电粒子进入场区后将向上偏转,并恰好从a板的右边缘处飞出;若撤去电场,在两金属板间加垂直纸面向里的匀强磁场,则相同的带电粒子从同一位置以相同的速度进入场区后将向下偏转,并恰好从b板的右边缘处飞出。现上述的电场和磁场同时存在于两金属板之间,仍让相同的带电粒子从同一位置以相同的速度进入场区,则下面的判断中正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.如下图所示,在平面直角坐标系xOy中的第一象限内存在磁感应强度大小为B、方向垂直予坐标平面向内的有界圆形匀强磁场区域(图中未画出);在第二象限内存在与x轴平行的匀强电场。一粒子源固定在x轴上的A点,A点坐标为(-L,0)。粒子源沿y 轴正方向释放出速度人小为v的电子,电子恰好能通过y轴上的C点,C点坐标为(0, 2L),电子经过磁场偏转后方向恰好垂直ON,ON是与x轴正方向成15°角的射线。(电子的质量为m,电荷量为e,不考虑粒子的重力和粒子之问的相互作用。)
求:
(1)第二象限内电场强度E的大小和方向。
(2)电子离开电场时的速度方向与y轴正方向的夹角θ。
(3)粗略画出电子在电场和磁场中的轨迹。
(4)圆形磁场的最小半径见
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24.如图所示,在平面直角坐标系xOy中的第一象限内存在磁感应强度大小为B、方向垂直于坐标平面向内的有界圆形匀强磁场区域(图中未画出);在第二象限内存在沿x轴负方向的匀强电场,一粒子源固定在x轴上的A点,A点坐标为(-L,0).粒子源沿y,轴正方向释放出速度大小为v的电子,电子恰好能通过y轴上的C点,(C点坐标为(0, 2L),电子经过磁场偏转后恰好垂直通过第一象限内与x轴正方向成15o角的射线ON(已知电子的质量为m,电荷量为e,不考虑粒子的重力和粒子之间的相互作用)。求:
(1)第二象限内电场强度E的大小
(2)电子离开电场时的速度方向与y轴正方向的夹角
(3)圆形磁场的最小半径Rm。
正确答案
(1)电子在从A运动到C的过程中,只受沿+x方向的电场力eE作用,故做类平抛运动,设其运动时间为t,因此在x方向上有:L=
在y方向上有:2L=vt ②
由①②式联立解得:E=
(2)根据类平抛运动的结论可知,电子离开电场时的速度的反向延长线将交于y方向位移的中点,即经过(-L,L)点,因此tanθ=1,θ=45°
(3)电子进入磁场后仅受洛伦兹力ev C B作用,在磁场中做匀速圆周运动,设其轨道半径为r,根据牛顿第二定律有:ev C B=
根据几何关系可知:v C =
根据题意作出电子的运动轨迹示意图如下图所示

由图中几何关系可知,电子在磁场中偏转120°后垂直于ON射出,因此当图中PQ为圆形磁场的直径时其半径最小,即有:R min =rsin60°⑤
由③④⑤式联立解得:R min =
解析
解析已在路上飞奔,马上就到!
知识点
23.如图所示,长为L的平行金属板M、N水平放置,两板之间的距离为d,两板间有水平方向的匀强磁场,磁感应强度为B,一个带正电的质点,沿水平方向从两板的正中央垂直于磁场方向进入两板之间,重力加速度为g。

(1)若M板接直流电源正极,N板接负极,电源电压恒为U,带电质点以恒定的速度v匀速通过两板之间的复合场(电场、磁场和重力场),求带电质点的电量与质量的比值。
(2)若M、N接如图所示的交变电流(M板电势高时U为正),L=0.5m,d=0.4m,B=0.1T,质量为m=1×10-4kg带电量为q=2×10-2C的带正电质点以水平速度v=1m/s,从t=0时刻开始进入复合场(g=10m/s2)
a.定性画出质点的运动轨迹

正确答案
(1) E=U/d
F电=qE;F磁=Bqv
由匀速:Bqv=qE+mg
得:q/m=g/(Bv-E)
(2)
a.
b.运动时间:t=L/v+2πm/Bq
t=0.814s
解析
解析已在路上飞奔,马上就到!
知识点
23.如图所示,地面上方竖直界面N左侧空间存在着水平的、垂直纸面向里的匀强磁场,磁感应强度B=2.0 T。与N平行的竖直界面M左侧存在竖直向下的匀强电场,电场强度E1=100N/C。在界面M与N之间还同时存在着水平向左的匀强电场,电场强度E2=200N/C。在紧靠界面M处有一个固定在水平地面上的竖直绝缘支架,支架上表面光滑,支架上放有质量m2=1.8×10-4kg的带正电的小物体b(可视为质点),电荷量q2=1.0×10-5 C。一个质量为m1=1.8×10-4 kg,电荷量为q1=3.0×10-5 C的带负电小物体(可视为质点)a以水平速度v0射入场区,沿直线运动并与小物体b相碰,a、b两个小物体碰后粘合在一起成小物体c,进入界面M右侧的场区,并从场区右边界N射出,落到地面上的Q点(图中未画出)。已知支架顶端距地面的高度h=1.0 m,M和N两个界面的距离L=0.10 m, g取10m/s2。
求:
(1)小球a水平运动的速率。
(2)物体c刚进入M右侧的场区时的加速度。
(3)物体c落到Q点时的动能。
正确答案
解(1)a向b运动过程中受向下的重力,向上的电场力和向下的洛仑兹力。小球a的直线运动必为匀速直线运动,a受力平衡,因此有
q1E1-q1v0B-m1g=0
解得v0=20m/s
(2)二球相碰动量守恒 
物体c所受洛仑兹力
物体c在M有场区受电场力F2=(q1-q2)E2=4×10-3N,方向向右
物体c受到的重力G=(m1+m2)g=3.6×10-3N,方向向下
物体c受到的合力F合=
物体c的加速度a=
设合力的方向与水平方向的夹角为θ,则tanθ=
加速度指向右下方与水平方向成45º角。
(3)物体c通过界面M后的飞行过程中电场力和重力都对它做正功。
设物体c落到Q点时的速率为
(m1+m2)gh+(q1-q2)E2L=
解得
解析
解析已在路上飞奔,马上就到!
知识点
24.如图所示,在直角坐标系的第一、二象限内有垂直于纸面的匀强磁场,第三象限有沿y轴负方向的匀强电场;第四象限无电场和磁场。现有一质量为m、电荷量为q粒子以速度v0从y轴上的M点沿x轴负方向进入电场,不计粒子的重力,粒子经x轴的N点和P点最后又回到M点,设OM=L,ON= 2L。求:
(1)电场强度E的大小;
(2)匀强磁场的磁感应强度的大小和方向;
(3)粒子从M点进入电场经N、P点最后又回到M点所用的时间。
正确答案
解:(1)粒子从M至N运动过程为类平抛运动,设运动时间为t1,根据运动的分解有:
x方向:
y方向:

联解①②③得:
(2)设粒子在N点时的速度vN与x轴成θ角,则由运动的合成与分解有:


设带电粒子在磁场中做匀速圆周运动的半径为R,圆心在O′处,过P点的速度方向与x夹角为θ′,作出轨迹如图所示。则由几何关系有:



由牛顿第二定律有:
联解⑤⑥⑦⑧⑨⑩得:
(3)粒子从M至N为类平抛运动,时间为t1;在磁场中做匀速圆周运动,时间为t2;从P至M做匀速直线运动,时间为t3。则有:




联解①⑾⑿⒀⒁⒂得: ⒃
解析
解析已在路上飞奔,马上就到!
知识点
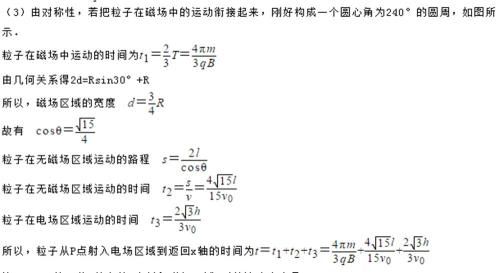
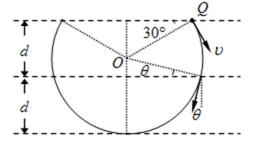
24.如图所示,在xOy平面内y>0的区域内分布着沿y轴负方向的匀强电场,在x轴下方有两个宽度相同且边界平行的条形匀强磁场区域,匀强磁场的磁感应强度大小均为B,方向垂直于xOy平面向外,磁场区域I的上边界与x轴重合,两个磁场区域的间距为l,质量为m、电荷量为q的带正电的粒子从y轴上的P点以初速度v0沿x轴正向射出,然后从x轴上的Q点射入磁场区域I。已知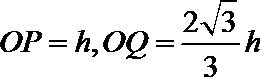

求:
(1)粒子从x轴上的Q点射入磁场区域I时的速度大小v;
(2)若粒子未从磁场区域I的下边界穿出,求条形磁场区域的最小宽度d0。
(3)若粒子恰好没从磁场区域II的下边界穿出,求粒子从P点射入电场区域到经过两个磁场区域后返回x轴的时间t
正确答案
(3)
解析
解析已在路上飞奔,马上就到!
知识点
24.如图甲所示,在光滑绝缘水平桌面内建立xoy坐标系,在第Ⅱ象限内有平行于桌面的匀强电场,场强方向与x轴负方向的夹角θ=45°。在第Ⅲ象限垂直于桌面放置两块相互平行的平板C1、C2,两板间距为d1=0.6m,板间有竖直向上的匀强磁场,两板右端在y轴上,板C1与x轴重合,在其左端紧贴桌面有一小孔M,小孔M离坐标原点O的距离为L=0.72m。在第Ⅳ象限垂直于x轴放置一块平行y轴且沿y轴负向足够长的竖直平板C3,平板C3在x轴上垂足为Q,垂足Q与原点O相距d2=0.18m。现将一带负电的小球从桌面上的P点以初速度


(1)匀强电场的场强大小;
(2)要使带电小球无碰撞地穿出磁场并打到平板C3上,求磁感应强度的取值范围;
(3)若t=0时刻小球从M点进入磁场,磁场的磁感应强度如乙图随时间呈周期性变化(取
竖直向上为磁场正方向),求小球从M点到打在平板C3上所用的时间。(计算结果保
留两位小数)
正确答案
(1)小球在第Ⅱ象限内做类平抛运动有:

带数据解得:
(2)设小球通过M点时的速度为v,
由类平抛运动规律:
小球垂直磁场方向进入两板间做匀速圆周运动,轨迹如图,
由牛顿第二定律有:
得:
小球刚好能打到Q点磁感应强度最强设为B1。此时小球的轨迹半径为R1
由几何关系有:
解得: 
小球刚好不与C2板相碰时磁感应强度最小设为B2,此时粒子的轨迹半径为R2
由几何关系有:
解得:
综合得磁感应强度的取值范围:
(3)小球进入磁场做匀速圆周运动,设半径为
由磁场周期
一个磁场周期内小球在x轴方向的位移为3r=0.54m
即:小球刚好垂直y轴
则在磁场中运动的时间
离开磁场到打在平板C3上所用的时间
小球从M点到打在平板C3上所用总时间
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析