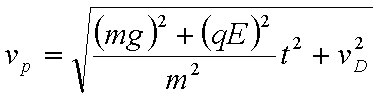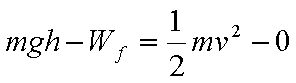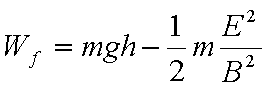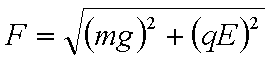- 带电粒子在混合场中的运动
- 共247题
如图所示,在两个水平放置的平行金属板之间,电场和磁场的方向相互垂直。一束带电粒子(不计重力)沿着直线穿过两板间的空间而不发生偏转。则这些粒子一定具有相同的
正确答案
解析
略
知识点
24.如图所示,直径分别为D和2D的同心圆处于同一竖直面内,O为圆心,GH为大圆的水平直径。两圆之间的环形区域(Ⅰ区)和小圆内部(Ⅱ区)均存在垂直圆面向里的匀强磁场。间距为d的两平行金属极板间有一匀强电场,上极板开有一小孔。一质量为m、电量为+q的粒子由小孔下方
(1)求极板间电场强度的大小;
(2)若粒子运动轨迹与小圆相切,求Ⅰ区磁感应强度的大小;
(3)若Ⅰ区、Ⅱ区磁感应强度的大小分别为

正确答案
(1)
(2)

(3)7πD;
解析:
由图可知,粒子每次从磁场Ⅱ区域进入Ⅰ区域速度方向偏离300,可知粒子往复转过12此后可再次经过H点;粒子一次循环走过的路程为
代入解得:
解析
解析已在路上飞奔,马上就到!
知识点
如图所示,正方形绝缘光滑水平台面WXYZ边长l=1.8m,距地面h=0.8m。平行板电容器的极板CD间距d=0.1m且垂直放置于台面。C板位于边界WX上,D板与边界WZ相交处有一小孔。电容器外的台面区域内有磁感应强度B=1T,方向竖直向上的匀强磁场。电荷量q=5×10-13C的微粒静止于W处,在CD间加上恒定电压U=2.5V,板间微粒经电场加速后由D板所开小孔进入磁场(微粒始终不与极板接触),然后由XY边界离开台面。在微粒离开台面瞬时,静止于X正下方水平地面上A点的滑块获得一水平速度,在微粒落地时恰好与之相遇。假定微粒在真空中运动、极板间电场视为匀强电场,滑块视为质点。滑块与地面间的动摩擦因数μ=0.2,取g=10m/s2。
(1)求微粒在极板间所受电场力的大小并说明两板的极性;
(2)求由XY边界离开台面的微粒的质量范围;
(3)若微粒质量m0=1×10-13kg,求滑块开始运动所获得的速度。
正确答案
见解析。
解析
(1)微粒在极板间所受电场力大小为F=
由微粒在磁场中的运动可判断微粒带正电荷,微粒由极板间电场加速,故C板为正极,D板为负极。
(2)若微粒的质量为m,刚进入磁场时的速度大小为v,由动能定理:Uq=
微粒在磁场中做匀速圆周运动,洛仑兹力充当向心力,若圆周运动半径为R,有:
微粒要从XY边界离开台面,则圆周运动的边缘轨迹如图所示,半径的极小值与极大值分别为
(3)如图,微粒在台面以速度v做以O点为圆心,R为半径的圆周运动,从台面边缘P点沿与XY边界成θ角飞出做平抛运动,落地点Q,水平位移s,下落时间t。设滑块质量为M,滑块获得速度v0后在t内沿与平台前侧面成ф角方向,以就爱上的a做匀减速直线运动到Q,经过位移为k。由几何关系,可得
cosθ=

对于滑块,由牛顿定律及运动学方程,有
μMg=Ma,
再由余弦定理:k2=s2+(d+Rsinθ)2-2s(d+Rsinθ)cosθ
及正弦定理:
联立并代入数据解得:v0=4.15m/s,ф=arcsin0.8(或ф=53°)
知识点
如图所示的平面直角坐标系xoy,在第Ⅰ象限内有平行于














(1)电场强度E的大小;
(2)粒子到达
(3)

正确答案
见解析
解析
(1)设粒子在电场中运动的时间为t,则有
联立以上各式可得
(2)粒子到达a点是沿负y方向的分速度为

(3)粒子在磁场中运动是,有
当粒子从b点射出是,磁场的磁感应强度为最小值,此时有
知识点
22. 如图,绝缘粗糙的竖直平面MN左侧同时存在相互垂直的匀强电场和匀强磁场,电场方向水平向右,电场强度大小为E,磁场方向垂直纸面向外,磁感应强度大小为B。一质量为m、电荷量为q的带正电的小
(1)求小滑块运动到C点时的速度大小vc;
(2)求小滑块从A点运动到C点过程中克服摩擦力做的功Wf;
(3)若D点为小滑块在电场力、洛伦兹力及重力作用下运动过程中速度最大的位置,当小滑块运动到D点时撤去磁场,此后小滑块继续运动到水平地面上的P点。已知小滑块在D点时的速度大小为vD,从D点运动到P点的时间为t,求小滑块运动到P点时速度的大小vp。
正确答案
(1)E/B (2
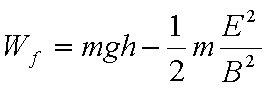
(1)由题意知,根据左手定则可判断,滑块在下滑的过程中受水平向左的洛伦兹力,当洛伦兹力等于电场力qE时滑块离开MN开始做曲线运动,即Bqv=qE
解得:v=E/B
(2)从A到C根据动能定理:
解得:
(3)设重力与电场力的合力为F,由图意知,在D点速度vD的方向与F地方向垂直,从D到P做类平抛运动,在F方向做匀加速运动a=F/m,t时间内在F方向的位移为
从D到P,根据动能定理: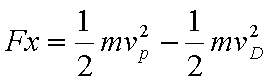
联立解得:
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析