- 平面向量的基本定理及其意义
- 共52题
24．将一圆的六个等分点分成两组相间的三点，它们所构成的两个正三角形扣除内部六条线段后可以形成一正六角星，如图所示的正六角星的中心为点
正确答案
解析
因为想求
①因为
②因为
③因为
④因为
所以
⑤因为
⑥因为
因此，
考查方向
本题主要考查向量的加法减法运算及几何意义
解题思路
表示向量，利用向量加法运算法则讨论，即可得到结果。A选项不正确，B选项不正确，D选项不正确，所以选C选项。
易错点
本题易在表示向量时发生错误。
知识点
7． O是平面上一定点，A、B、C平面上不共线的三点，动点P满足
正确答案
解析
由
再由共线定理知点
考查方向
解题思路
先对原式变形可得
所以
再由共线定理知点
易错点
1、不理解向量
2、对三角形的各心与对应线没有对应起来。
知识点
6.设
A
B
C
D
正确答案
解析
以
∴
∴
考查方向
解题思路
该题属于常规题1、把
易错点
主要易错不能有效理解BCD的关系
知识点
P是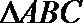
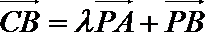
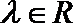
A
BAC边所在直线上
CAB边所在直线上
DBC边所在直线上
正确答案
解析
由已知，得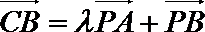
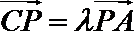
考查方向
本题主要考查了向量的基本运算以及平面几何的综合应用
易错点
向量基本运算需要仔细运算
知识点
4. 在
A
B
C
D
正确答案
解析
由
所以，
考查方向
本题考查了向量的线性运算及三角形法则等知识。
解题思路
由
易错点
向量的三角形法则不能熟练掌握，导致运算错误。
知识点
16.在平面直角坐标系中，设
正确答案
解析
因为
即是
画出可行域如图
又因为，
上式可看成是点（a,b）与点(0,-1)距离的平方和加上点（a,b）与点(0,-1)连线的斜率再减掉1，由图可知，在点（1，0）处它们同时取得最小值，代入可得最小值为2，即取值范围为
考查方向
本题是解析几何，向量，线性规划的高难度综合题，属于难题。
解题思路
（1）作出点(a,b)的可行域。
（2）找出式子
易错点
（1） 易忽视“点
（2）对向量
（3）对
知识点
6．如图，在△OAB中，点P在边AB上，且AP：PB=3：2．则
A
B
C
D
正确答案
考查方向
易错点
1、本题在AP：PB=3：2变换成
知识点
设
A
B
C
D
正确答案
解析
这类题型需要建立好坐标系，根据坐标系找可行域更可行
考查方向
向
解题思路
先建立直角坐标系，然后求出EC和CD的方程，找到可行域，将平面向量用坐标形式表示，带入可行域中，求得。
易错点
建立坐标系错误、计算能力弱
知识点
3．如图，正方形
A
B
C
D
正确答案
解析
考查方向
本题主要考察了平面向量的基本定理，属于中档题，是高考的热点，解决此类题的关键是会利用平面向量的基本定理，用两个不共线的向量表示平面内任一向量。
易错点
本题易在向量的表示过程中出现错误。
知识点
16．已知点A（0，－1），B（3，0），C（1，2），平面区域P是由所有满足
正确答案
解析
由题可知，设M（x,y），则
8<x≤3m+n,7<y≤m+3n-1，画出平面区域，利用面积公式可得（m+n）min=
考查方向
本题主要考查线性规划及向量的线性运算。
解题思路
1、画出平面区域
2、化简公式求解．
易错点
本题必须注意利用图像完成。
知识点
扫码查看完整答案与解析